জ্যামিতি হল স্পর্শস্থান এবং তার সম্পর্কিত বিষয় সম্পর্কে বিশেষভাবে গবেষণা করা । জ্যামিতির তিনটি মৌলিক উপাদান হল বিন্দু, রেখা এবং কোণ। বিন্দু হল একটি স্থান, যার কোন আকার না থাকলেও স্থানীয় স্থান নির্দেশ করে। রেখা হল দুটি বিন্দুকে সংযোজন করা একটি সরল সেগমেন্ট এবং এটির দৈর্ঘ্য হল বিন্দু দুটির মধ্যবর্তী দূরত্ব। কোণ হল দুটি রেখার মধ্যে উৎপন্ন বাহুর মাধ্যমে উৎপন্ন একটি পরিমাপযুক্ত জোড়া রেখা। জ্যামিতির উপর ভিত্তি করে বিভিন্ন ধরনের আকার ও গণিতগত প্রসঙ্গ নির্ণয় করা হয়। জ্যামিতি ব্যবহার করে বিভিন্ন ফিজিক্স, গণিত এবং প্রকৃতি বিজ্ঞানের প্রযুক্তি তৈরি করা হয়। জ্যামিতি আমাদের জীবনে কতটা গুরুত্বপূর্ণ হবে সেটি আমাদের সবার আগে জানতে হবে।
প্রাথমিক আলোচনা
জ্যামিতি গণিত শাস্ত্রের একটি প্রাচীন শাখা। যদিও ব্যুৎপত্তিগতভাবে "জ্যামিতি" শব্দের অর্থ ভূমির পরিমাপ তথা জ্যামিতি, প্রকৃত পক্ষে স্থান বিষয়ক বিজ্ঞান (Geometry is the science concerned with space) ভূমি পরিমাপের জন্য জ্যামিতির উদ্ভব হলেও বর্তমানে জ্যামিতি কেবল ভূমি পরিমাপের জন্যই ব্যবহৃত হয় না বরং বহু জটিল গাণিতিক সমস্যা সমাধানে জ্যামিতিক জ্ঞান অপরিহার্য। জ্যামিতিক জ্ঞান আমাদের জীবনের সমস্যা সমাধানের ইঙ্গিত দেয়, চিন্তা শক্তির উন্মেষ ও মননশীলতার উৎকর্ষ সাধন করে থাকে। জ্যামিতি বা Geometry শব্দের 'জ্যা' এর অর্থ ভূমি এবং 'মিতি' এর অর্থ পরিমাপ অর্থাৎ 'ভূমির পরিমাপ'। (The word 'geometry' means 'earth measure') আরো বলা যায়, “গণিতশাস্ত্রের যে শাখায় বিন্দু থেকে বৃত্ত পর্যন্ত যাবতীয় ক্ষেত্রের বৈশিষ্ট্য ধর্ম এবং ক্ষেত্রের পরিমাপ সম্বন্ধে আলোচিত হয় তারই নাম জ্যামিতি। খ্রিষ্টপূর্ব ৩০০ সালে ইউক্লিড তার The Elements গ্রন্থে জ্যামিতির মূল তত্বগুলো আলোচনা করেছেন।
বিন্দু (Points)
যার কেবল অবস্থান আছে কিন্তু দৈর্ঘ্য, প্রস্থ, উচ্চতা বা বেধ বলতে কিছুই নেই তাকে বিন্দু বলে। দৈর্ঘ্য, প্রস্থ এবং উচ্চতা কোনো কিছুই নেই বলে বিন্দুর কোনো মাত্রা নেই অর্থাৎ, বিন্দুর মাত্রা শুন্য।
বিন্দুর শুধু অবস্থান আছে কিন্তু কোন মাত্রা নেই ।
দুটি বিন্দুর মধ্য দিয়ে একটি এবং কেবলমাত্র সরলরেখা আঁকা যায়।
দুটি সরলরেখা একটি এবং কেবল একটি বিন্দুতে পরস্পরকে ছেদ করতে পারে।
দুই বিন্দুর মধ্যে সরলরেখার দূরত্বই ক্ষুদ্রতম ।
যেসব বিন্দু একই সরলরেখায় অবস্থান করে, তাদেরকে সমরেখ বিন্দু বলে ।
রেখা (Line)
রেখা : বিন্দুর চলার পথকে রেখা বলে ।
সমরেখ:
যখন দুই-এর অধিক বিন্দু একই সরলরেখার উপর অবস্থিত হয়, তখন ঐ বিন্দুগুলিকে সমরেখ বিন্দু বলা হয়। চিত্রে
A, B, C বিন্দু তিনটি সমরেখ ।
রেখার কোন প্রান্ত বিন্দু নেই ।
রেখাংশের দুটি প্রান্তবিন্দু থাকে ।
রশ্মির একটিমাত্র প্রান্তবিন্দু থাকে।
সরলরেখা (Straight Line): একটি বিন্দু থেকে অন্য একটি বিন্দুতে পৌছাতে যদি কোনো প্রকার দিকের পরিবর্তন না হয় তবে তাকে সরল রেখা বলে ।
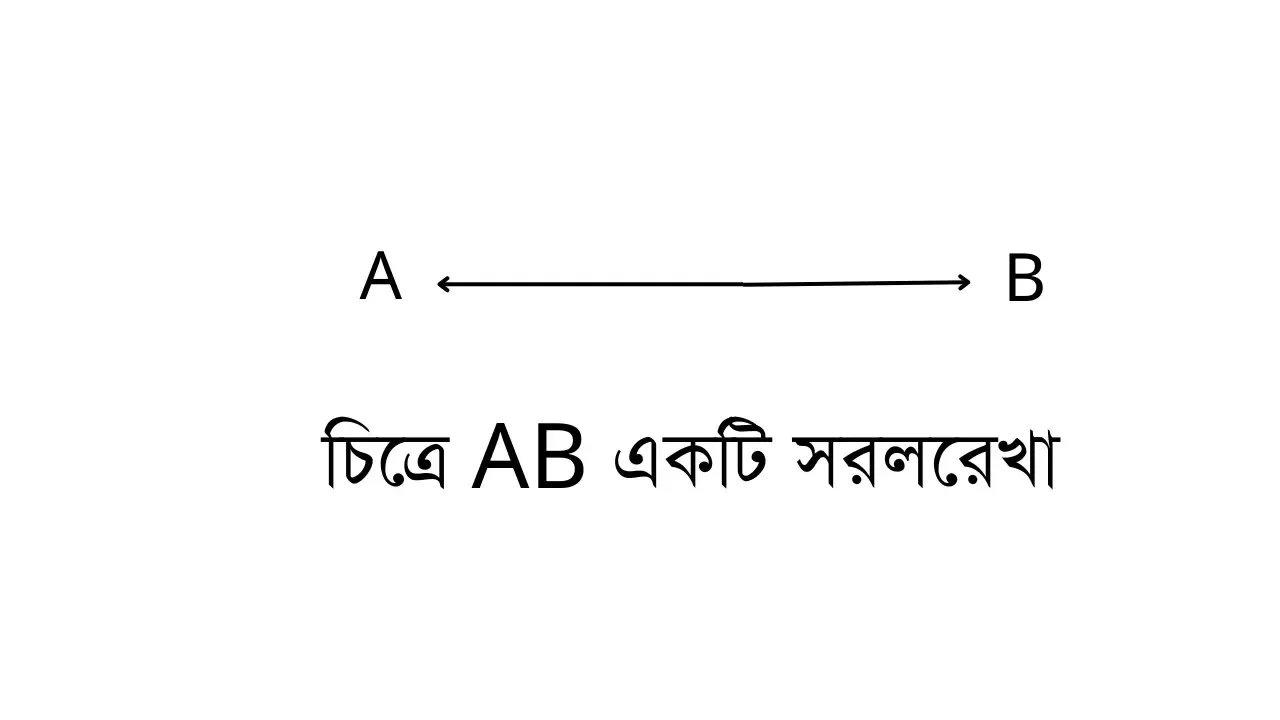
দুটি বিন্দু দিয়ে একটি মাত্র সরলরেখা আঁকা যায় ।
একটি সরলরেখার বহিঃস্থ যে কোনো বিন্দু থেকে ঐ সরলরেখা পর্যন্ত যেসব সরলরেখা আঁকা যায়, তাদের মধ্যে লম্বের দৈর্ঘ্যই ক্ষুদ্রতম ।
বক্র রেখা (Zigzag line ): একটি বিন্দু থেকে অন্য একটি বিন্দুতে পৌছাতে যদি দিক পরিবর্তন হয় তবে তাকে বক্র রেখা বলে ।
সমান্তরাল রেখা (Parallel Lines):
দুটি রেখা যদি পরস্পরের মধ্যে সর্বদা সমান দূরত্ব বজায় রেখে চলতে থাকে তবে তাকে সমান্তরাল রেখা বলে ।
কোন সরলরেখার বহিঃস্থ কোন বিন্দু থেকে উক্ত রেখা পর্যন্ত যতগুলো রেখাংশ টানা যায় তন্মধ্যে লম্ব রেখাংশটিই ক্ষুদ্রতম ।
দুইটি সমান্তরাল সরলরেখার কোন সাধারণ বিন্দু নেই ।
দুটি পরস্পরচ্ছেদী সরলরেখার প্রত্যেকটি, কোন তৃতীয় সরলরেখার সমান্তরাল হতে পারে না।
যেসব সরলরেখা একই সরলরেখার সমান্তরাল তারা পরস্পর সমান্তরাল। দুই বা ততোধিক সরলরেখা একটি সরলরেখার উপর লম্ব হলে, তারা পরস্পর সমান্তরাল ।
একটি সরলরেখা সমান্তরাল রেখাদ্বয়ের একটির উপর লম্ব হলে, তা অপরটির উপরও লম্ব।
কোণ (Angle):
কোণ (Angle): দুটি সরলরেখা তির্যকভাবে (আড়াআড়িভাবে) পরস্পরের সাথে মিলিত হলে মিলিত বিন্দুতে কোণ উৎপন্ন হয়। নিচের চিত্র দেখুন ।
সমকোণ (Right Angle): যে কোণের পরিমাণ 90 ডিগ্রী তাকে সমকোণ বলে । নিচের চিত্র দেখুন ।
মনে রাখুন: কোণটি দেখতে যে রকমই হোক না কেন তার পরিমাপ 90 ডিগ্রী হলেই তাকে সমকোণ বলা হবে।
স্থূলকোণ (Obtuse Angle ) : যে কোণের পরিমাণ ৯০ ডিগ্রী অপেক্ষা বেশী এবং ১৮০ ডিগ্রি অপেক্ষা কম তাকে স্থূলকোণ বলে । নিচের চিত্র দেখুন ।
সূক্ষ্মকোণ (Acute Angle ) : যে কোণের পরিমাণ 90 ডিগ্রী অপেক্ষা কম তাকে সূক্ষ্মকোণ বলে । নিচের চিত্র দেখুন ।
সরলকোণ (Straight Angle ) : যে কোণের পরিমাণ ১৮০ ডিগ্ৰী তাকে সরলকোণ বলে । নিচের চিত্র দেখুন ।
<_____________________>
চিত্র : সরলকোণ
প্রবৃদ্ধ কোণ (Reflex Angle ) : যে কোণের পরিমাণ দুই সমকোণ ( 180 ডিগ্রি ) অপেক্ষা বেশী কিন্তু চার সমকোণ ( 360 ডিগ্রি ) অপেক্ষা কম তাকে প্রবৃদ্ধ কোণ বলে। নিচের চিত্র দেখুন ।
বিপ্রতীপ কোণ (Vertically Opposite Angle) : দুইটি সরলরেখা পরস্পরকে ছেদ করলে ছেদবিন্দুতে যে চারটি কোণ উৎপন্ন হয় তাদের একটিকে অপরটির বিপ্রতীপ কোণ বলে।
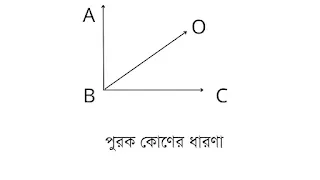
পুরক কোণ (Complementary Angle) : দুইটি কোণের সমষ্টি এক সমকোণ বা ৯০ ডিগ্রি হলে একটিকে অপরটির পূরক কোণ বলে।
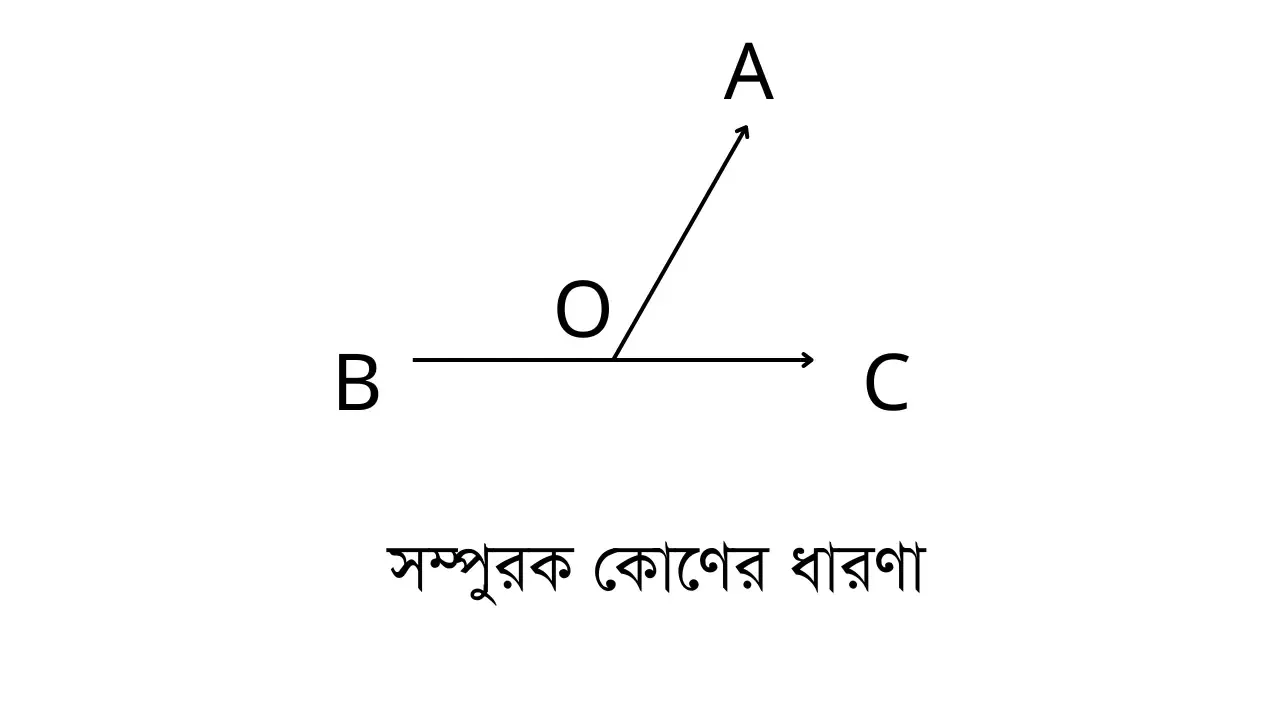
সম্পুরক কোণ (Complementary Angle) : দুইটি কোণের সমষ্টি দুই সমকোণ বা ১৮০ ডিগ্রি হলে একটিকে অপরটির সম্পুরক কোণ বলে।
সন্নিহিত কোণ (Adjacent Angle): দুইটি কোণের শীর্ষবিন্দু একই হলে সাধারণ বাহুর উভয় পাশের কোণদ্বয়কে সন্নিহিত কোণ বলে । অর্থাৎ পাশাপাশি লাগানো দুটি কোণকে সন্নিহিত কোণ বলে ।
অন্তর্ভুক্ত কোণ: দুটি বাহুর মিলিত হওয়ার স্থানকে ঐ বাহুদ্বয়ের অন্তর্ভুক্ত কোণ বলা হয়।
একান্তর' কোণ (Alternative Angle): দুটি সমান্তরাল সরলরেখাকে অপর একটি রেখা তির্যকভাবে (আড়াআড়ি) ছেদ করলে ছেদক রেখার বিপরীত পার্শ্বে সমান্তরাল রেখা যে কোণ উৎপন্ন করে তাকে একান্তর কোণ বলে ।
একান্তর কোণদ্বয় পরস্পর সমান হয়।
অনুরূপ কোণ (Corresponding Angle) : দুটি সমান্তরাল সরলরেখাকে অপর একটি সরলরেখা তির্যকভাবে ছেদ করলে ছেদক রেখার একই দিকে সমান্তরাল রেখাদ্বয়ের অনুরূপ পার্শ্বে যে কোণ উৎপন্ন হয়, তাকে অনুরূপ কোণ বলে ।
অনুরুপ কোণ দেখতে একই রকম এবং অনুরুপ কোণগুলো পরস্পর সমান ।
অন্তঃস্থ কোণ (Interior Angles): যে কোন ত্রিভুজ, চতুর্ভুজ অথবা বহুভুজের অভ্যন্তরে বা ভেতরে যে কোণ উৎপন্ন হয় তাকে অন্তঃস্থ কোণ বলে ।
বহিঃস্থ কোণ (Exterior Angles) : কোন ত্রিভুজ, চতুর্ভুজ অথবা বহুভুজের যে কোণ এক বাহু বর্ধিত করলে বাহিরে যে কোণ উৎপন্ন হয় তাকে বহিঃস্থ কোণ বলে ।