ত্রিভুজ কাকে বলে? ত্রিভুজ কত প্রকার ও কি কি? mcq সহ এ টু জেড

ত্রিভুজ হলো তিনটি বাহু বা সাইড দ্বারা গঠিত একটি আবদ্ধ চিত্র বা ক্ষেত্র। যা তিনটি বিন্দুতে স্থাপিত হয় । এটি ব্যবহার করা হয় বিভিন্ন ধরনের গণিত ও জ্যামিতিক সমস্যার সমাধানের জন্য। একটি ত্রিভুজের মোট তিনটি কোণ এবং তিনটি বাহু থাকে। যেহেতু তিনটি বিন্দু সমান্তরাল হতে পারে না, সুতরাং ত্রিভুজের ক্ষেত্রফল হলো বিন্দু দুইটির লম্বদূরত্ব গুণ করে সংখ্যাগুলোর সমান ভাগফল। ত্রিভুজের বাহুর দৈর্ঘ্য বা কোণের মান জানতে হলে ত্রিভুজের অংকে প্রয়োজনীয় সূত্রগুলো ব্যবহার করা হয়। ত্রিভুজ বিষয়ক জ্যামিতি অনেক কঠিন হওয়ার কারণে এর সমস্যা সমাধান এবং উপযোগিতা বিষয়ক অনেক গবেষণা চলছে। তবে ত্রিভুজ বিষয়ক জ্ঞান সম্পর্কে স্পষ্ট ধারণা নিতে হলে আজকের এই টিউটরিয়ালটি আপনার মনোযোগ সহকারে পড়া উচিত।

প্রাথমিক আলোচনা
ত্রিভুজ বিষয়ক গুরুত্বপূর্ণ অনুসিদ্ধান্ত
ত্রিভুজের সর্বসমতা
ত্রিভুজের কেন্দ্র
ত্রিভুজের প্রকারভেদ
বিভিন্ন প্রতিযোগিতামূলক পরীক্ষার প্রশ্ন ও সমাধান

প্রাথমিক আলোচনা

ত্রিভুজ: তিনটি বাহু দ্বারা আবদ্ধ চিত্র বা ক্ষেত্রকে ত্রিভূজ বলে।

চিত্রে ABC একটি ত্রিভুজ। এখানে AB, BC ও AC তিনটি বাহু দ্বারা ABC একটি আবদ্ধ চিত্র হয়েছে যাকে ত্রিভুজ বলা যায় ।

ত্রিভুজ সম্পর্কে বিস্তারিত জানার আগে আমরা ত্রিভুজের সাথে সংশ্লিষ্ট কয়েকটি টার্ম জেনে নেই । যথা:

ভূমি (Base): চিত্রে BC হলো ভূমি।

শীর্ষবিন্দু (Vertex): চিত্রে A হল শীর্ষবিন্দু।

অন্তঃস্থ কোণ: চিত্রে ABC ত্রিভুজ ক্ষেত্রের ভিতরের যে তিনটি কোণ ∠A, ∠B, ∠C উৎপন্ন হয়েছে তা অন্তঃস্থ কোণ ।

বহিঃস্থকোণ: △ABC চিত্রের বাহিরে যে ∠ACD কোণ উৎপন্ন হয়েছে তা বহিঃস্থকোণ।

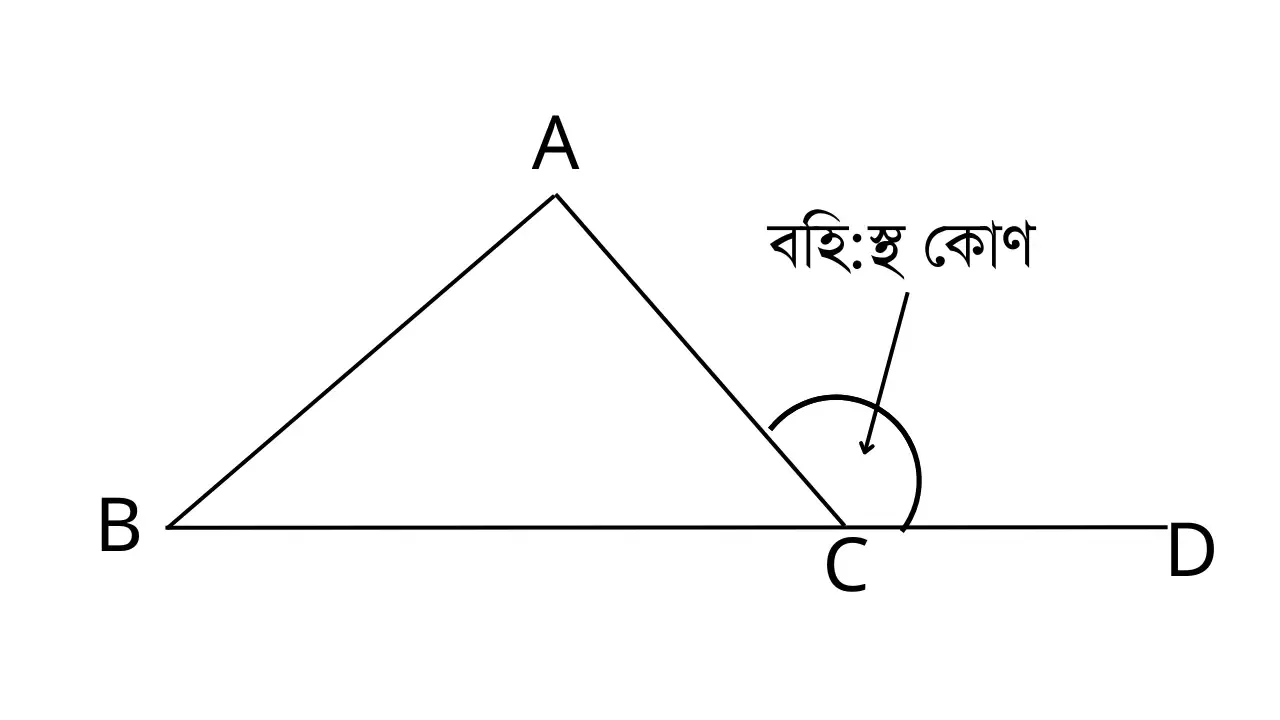বহিঃস্থ কোণ উচ্চতা: ত্রিভুজের শীর্ষবিন্দু থেকে ভূমির উপর অঙ্কিত লম্বের দৈর্ঘ্যকে উচ্চতা বলে । চিত্রে AD হল ABC ত্রিভুজের উচ্চতা।

মধ্যমা: ত্রিভুজের শীর্ষ বিন্দু থেকে ভূমির মধ্যবিন্দুর সংযোগ রেখাকে মধ্যমা বলে। চিত্রে AD হল মধ্যমা; কেননা AD, BC বাহুকে ২ ভাগে ভাগ করেছে। এছাড়াও B ও C বিন্দুকে শীর্ষবিন্দু ধরে আরো দুটি মধ্যমা অঙ্কন করা যায় ।

ত্রিভুজ বিষয়ক গুরুত্বপূর্ণ অনুসিদ্ধান্ত

ত্রিভুজের বিভিন্ন বৈশিষ্ট্য ও শর্তের উপর নিম্নলিখিত অনুসদ্ধিান্ত গুলো অত্যন্ত গুরুত্বপূর্ণ কেননা এই নিয়মগুলির উপর ভিত্তি করেই বিভিন্ন ধরনের প্রশ্ন তৈরী করা যায় এবং সেভাবেই বিভিন্ন পরীক্ষায় ও আসে। তাই চিত্র দেখে বুঝে বুঝে পড়ুন এবং লিখুন। পাশাপাশি নিয়ম সংশ্লিষ্ট প্রশ্নগুলো সমাধান করুন ।

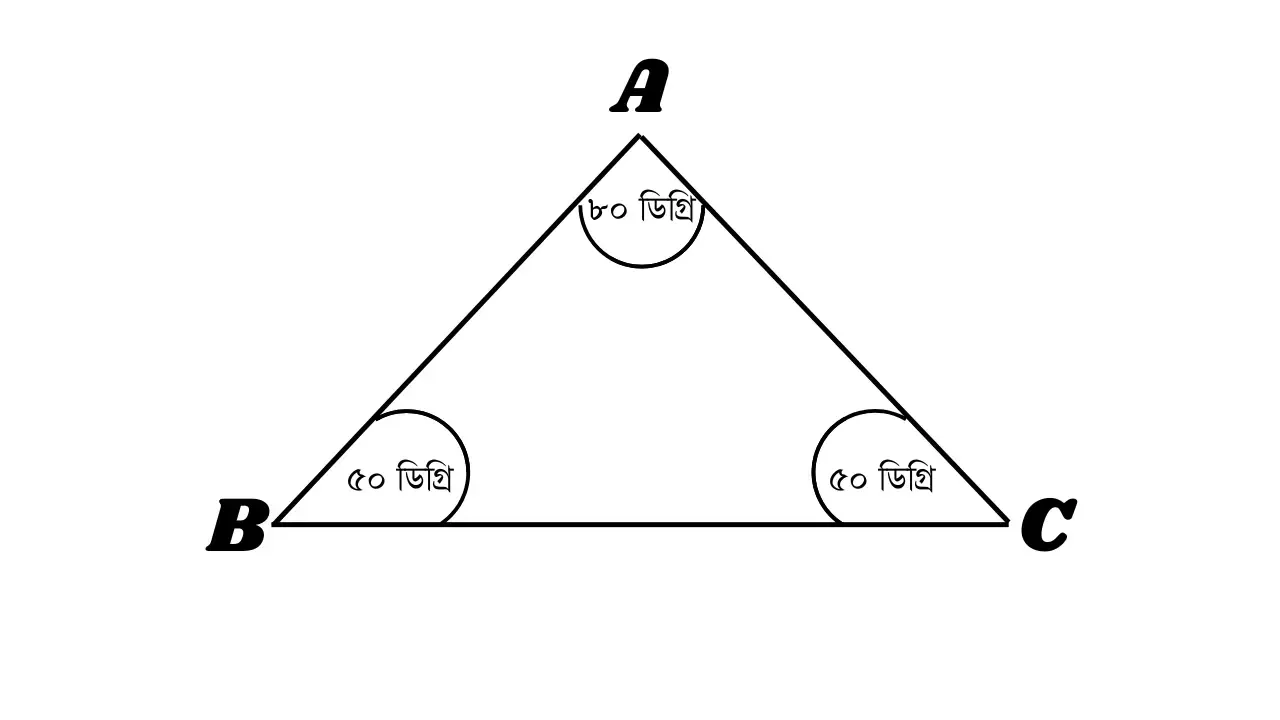
অনুসিদ্ধান্ত - ০১: ত্রিভুজের তিন কোণের সমষ্টি ১৮০ ডিগ্রি অর্থাৎ ২ সমকোণ । চিত্রে: ∠A + ∠B + ∠C = ১৮০ ডিগ্রি বা ২ সমকোণ।
এজন্য যে কোন একটি কোণের পরিমাণ দেয়া না থাকলে অপর দুটি কোণের পরিমাণ যোগ করে 180 ডিগ্রি থেকে তা বিয়োগ করলে তৃতীয় কোণের পরিমাণ বের হবে।

অনুসিদ্ধান্ত - ০২: ত্রিভুজের যেকোন দুই বাহুর সমষ্টি,তার তৃতীয় বাহু অপেক্ষা বৃহত্তর, অর্থাৎ ত্রিভুজের যে কোন দুটি বাহু যোগ করলে তা তৃতীয় বাহু অপেক্ষা বড় হতে হবে। যদি বৃহত্তর না হয় তাহলে তা ত্রিভুজ হবে না। যেমন:
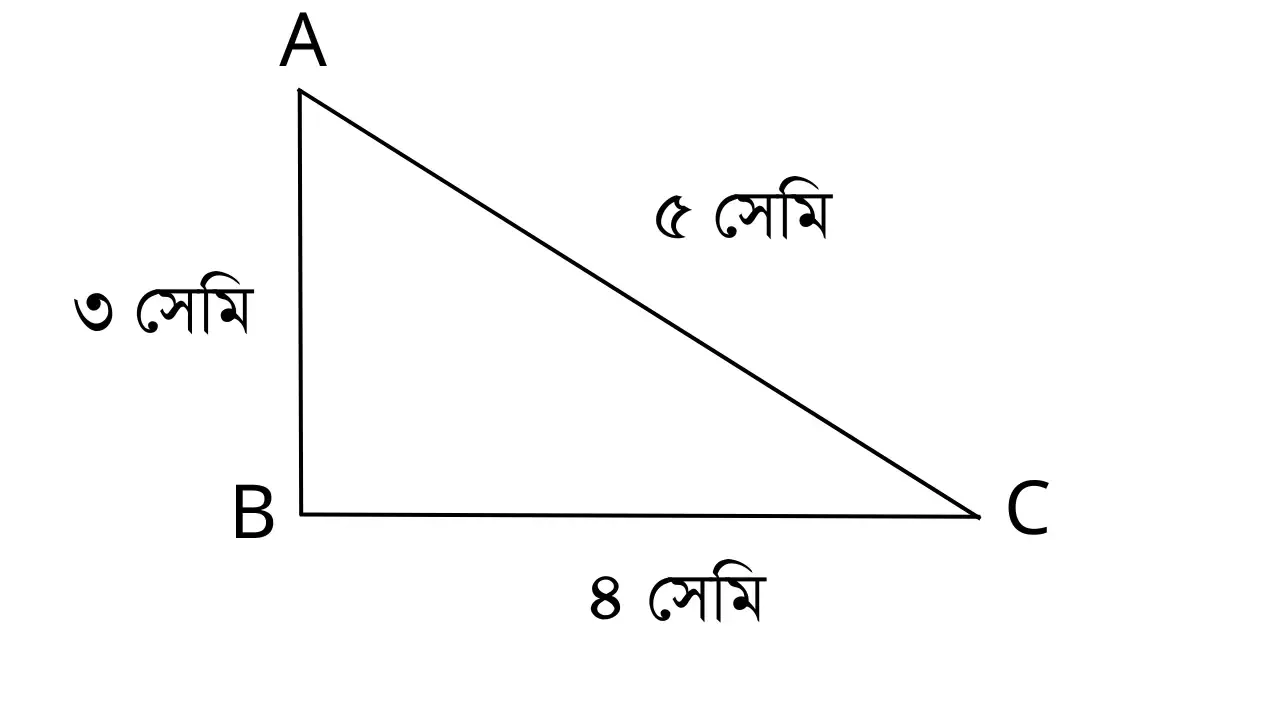উপরের চিত্রে AB = ৩ সে.মি., BC = ৪ সে. মি. এবং AC = ৫ সে. মি. তাহলে, ৩+ ৪ > ৫ বা, ৭ > ৫ অর্থাৎ AB + BC > AC অন্য পাশ থেকে অন্য যে কোন দুটি বাহু নিলেও তাদের যোগফল ৩য় বাহু থেকে বড় হবে ।

অনুসিদ্ধান্ত – ০৩: ত্রিভুজের যেকোন দুই বাহুর অন্তর, তৃতীয় বাহু অপেক্ষা ক্ষুদ্রতর, অর্থাৎ ত্রিভুজের দুটি বাহু বিয়োগ করলে যেন তা তৃতীয় বাহু থেকে ছোট হয়। উপরের চিত্রে AB = ৩ সে. মি., BC = ৪ সে. মি. এবং AC = ৫ সে. মি. তাহলে, ৫- ৩< ৪ এবং ২ < ৪ সুতরাং বলা যায়, AC - AB < BC

বোঝার জন্য: একটি ত্রিভুজের তিনটি বাহুর দৈর্ঘ্য যথাক্রমে ৫, ৮ এবং ১২ এখানে যে কোন দুটি বাহু বিয়োগ করলে তা তৃতীয় বাহু অপেক্ষা ছোট হবে। কিন্তু যদি বলা হয় তিনটি বাহুর দৈর্ঘ্য যথাক্রমে ৩,৫,১২ তখন তা ত্রিভুজ হবে না, কারণ এখানে ১২- ৫ = ৭ হয় যা তৃতীয় বাহু ৩ থেকে বড়।

অনুসিদ্ধান্ত-০৪: ত্রিভুজের কোনো শীর্ষ বিন্দু থেকে তার বিপরীত বাহুর মধ্যবিন্দুর সংযোজক সরলরেখাকে মধ্যমা বলে।
Confusion Clear: শীর্ষ বিন্দু অর্থ শুধু উপরের বিন্দু নয়, এবং ত্রিভুজের যেকোনো একটি বাহুকে ভূমি কল্পনা করলে ভূমির বিপরীত বিন্দুকে শীর্ষ বিন্দু বলে ।

মধ্যমা সংক্রান্ত গুরুত্বপূর্ণ তথ্য:
(i) ১টি ত্রিভুজের ৩টি মধ্যমা থাকে ।
(ii) যেকোন মধ্যমা ত্রিভুজের ক্ষেত্রফলকে সমান দুই ভাগে ভাগ করে।
(iii) ত্রিভুজের মধ্যমাগুলোর সমষ্টি ত্রিভুজের পরিসীমা অপেক্ষা ক্ষুদ্রতর।

অনুসিদ্ধান্ত -০৫ : কোন ত্রিভুজের বৃহত্তর বাহুর বিপরীত কোণ বৃহত্তম আবার বৃহত্তম কোণের বিপরীত বাহু বৃহত্তর ।

অনুসিদ্ধান্ত -০৬ : কোন ত্রিভুজের সমান সমান বাহুর বিপরীত কোণগুলোও পরস্পর সমান আবার সমান সমান কোণের বিপরীত বাহুগুলোও সমান হবে ।

অনুসিদ্ধান্ত-০৭: ত্রিভুজের একটি বাহু বর্ধিত করলে যে বহিঃস্থ কোণ উৎপন্ন হয় তা বিপরীত অন্তঃস্থ কোণদ্বয়ের সমষ্টির সমান।

অনুসিদ্ধান্ত-০৮ : ত্রিভুজের বহিঃস্থ কোণগুলোর যোগফল ৪ সমকোণ বা ৩৬০ ডিগ্রি। সুতরাং ত্রিভুজের যে কোন দুটি বহিঃস্থ কোণের সমষ্টি দুই সমকোণ অপেক্ষা বৃহত্তর হবে। মনে রাখুন: যে কোন বহুভুজের ক্ষেত্রে ( চতুর্ভুজ, পঞ্চভুজ,ষড়ভুজ-ইত্যাদির ক্ষেত্রেও) বহিঃস্থ কোণগুলোর সমষ্টি ৩৬০ ডিগ্রি হয়।

অনুসিদ্ধান্ত- ০৯: ত্রিভুজের যেকোন দুইবাহুর মধ্যবিন্দুর সংযোজক সরলরেখা তৃতীয় বাহুর সমান্তরাল ও অর্ধেক।

ত্রিভুজের সর্বসমতা

দুটি ত্রিভুজ সর্বসম হওয়া অর্থ হল ত্রিভুজ দুটির আকার, আকৃতি ও ক্ষেত্রফল সমান হওয়া । তাই দুটি ভিন্ন ভিন্ন ক্ষেত্রের ক্ষেত্রফল সমান হলেও তাদের আকৃতি সমান না হলে ত্রিভুজ দুটি যেমন সর্বসম হবে না। তেমনি, দুটি ত্রিভুজ যদি দেখতে একই রকম মনে হয় কিন্তু তাদের ক্ষেত্রফল সমান নয় তাহলেও ত্রিভুজ দুটি সর্বসম হবে না।
সর্বসম: আকার, আকৃতি ও ক্ষেত্রফল সমান হতে হবে।

দুটি ত্রিভুজের সর্বসমতার শর্ত: নিম্নোক্ত শর্তগুলো পূরণ হলে দুটি ত্রিভুজ সর্বসম হয়।

ক. দুই বাহু ও অন্তর্ভুক্ত কোণ সমান
খ. তিনবাহু সমান
গ. দুই কোণ ও এক বাহু সমান
ঘ. সমকোণী ত্রিভুজের অতিভুজ ও এক বাহু সমান
সর্বসমতা নির্দেশক চিহ্ন ≅

দুটি ত্রিভুজ কখন সর্বসম হয় না ?
ক. যখন তাদের ক্ষেত্রফল সমান হয় কিন্তু আকৃতি সমান হয় না। চিত্র দেখে বুঝুন -
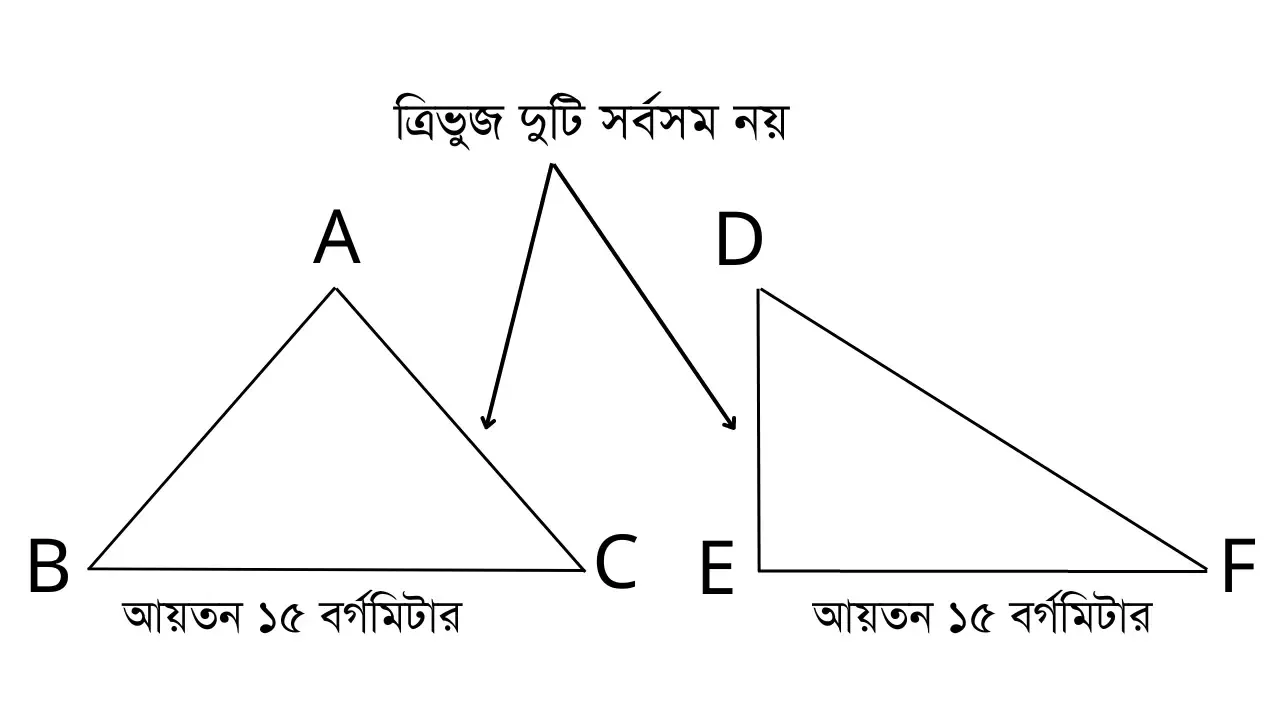ত্রিভুজের সর্বসমতা খ. আবার দুটি ত্রিভুজের আকৃতি দেখতে একই রকম হয় কিন্তু ক্ষেত্রফল সমান হয় না ৷ চিত্র দেখে বুঝুন -
ত্রিভুজের সর্বসমতা গ. আবার একটি ত্রিভুজের তিনটি কোণ অপর একটি ত্রিভুজের তিনটি কোণের সমান হওয়া সত্ত্বেও ত্রিভুজ দুটি সর্বসম না ও হতে পারে। যেমন: চিত্রটি দেখুন: -
ত্রিভুজের সর্বসমতা এই দুটি ত্রিভুজ সর্বসম নয় ।কারণ কোণগুলো সমান হলে ও বাহুগুলো কিন্তু সমান নয় । এরুপ সমান কোণ বিশিষ্ট দুটি ত্রিভুজকে সদৃশ্যকোণী ত্রিভুজ বলা হয়।

ত্রিভুজের কেন্দ্র

অন্ত:কেন্দ্র (In-centre): ত্রিভূজের কোণের সমদ্বিখন্ডিত বাহুত্রয় যে বিন্দুতে মিলিত হয় তাকে অন্তঃকেন্দ্র বলে ।
অন্তকেন্দ্র চিত্রঃ- অন্ত:কেন্দ্র
△ABC- এ ∠A, ∠B ও ∠C কোণের সমদ্বিখন্ডক বাহুত্রয়ের মিলিত বিন্দু O। আর O হল ত্রিভূজটির অন্তঃকেন্দ্র।

পরিকেন্দ্র (Circumcentre) : ত্রিভূজের বাহু বা পরিসীমার উপর অঙ্কিত লম্বত্রয় ত্রিভূজের অভ্যন্তরে যে বিন্দুতে মিলিত হয় তাকে পরিকেন্দ্র বলে ।
চিত্রঃ- পরিকেন্দ্র
△ABC- এ AB, BC ও AC বাহুত্রয়ের উপর লম্ব ত্রয় যথাক্রমে OP, OQ,OR । অতএব O হল পরিকেন্দ্র।

ভরকেন্দ্র (Centroid): ত্রিভূজের শীর্ষবিন্দু হতে বিপরীত বাহুর মধ্যবিন্দুর সংযোগ সরলরেখাত্রয় যে বিন্দুতে মিলিত হয় তাকে ভরকেন্দ্র বলে।
চিত্রঃ- ভরকেন্দ্র
ব্যাখ্যা: চিত্রে △ABC-এ A,B ও C শীর্ষবিন্দু এবং তাদের বিপরীত বাহুত্রয় হল BC,AC,AB। এখন শীর্ষ বিন্দু থেকে বাহুত্রয়ের মধ্যবিন্দুর সংযোগ সরলরেখাত্রয় হল- AQ,BR,CP । রেখাত্রয় মিলিত হয়েছে O বিন্দুতে । অতএব O হল ত্রিভূজের ভরকেন্দ্র।

ত্রিভুজের প্রকারভেদ

ত্রিভুজকে প্রধানত ২টি বৈশিষ্ট্যের ভিত্তিতে ভাগ করা যায়। যথা:
১. কোণ ভেদে
২. বাহুভেদে

১. কোণভেদে ত্রিভুজ ৩ প্রকার । যথা:
(i) সমকোণী ত্রিভুজ
(ii) সূক্ষ্মকোণী ত্রিভুজ
(iii) স্থূলকোণী ত্রিভুজ

২. বাহুভেদে ত্রিভুজ ৩ প্রকার। যথা:
(i) সমবাহু ত্রিভুজ
(ii) সমদ্বিবাহু ত্রিভুজ
(iii) বিষমবাহু ত্রিভুজ

সমকোণী ত্রিভুজ (Right angled triangle):

[সমকোণী ত্রিভুজের উপর সবথেকে বেশি প্রশ্ন হয়ে থাকে ।]

যে ত্রিভুজের একটি কোণ সমকোণ তাকে সমকোণী ত্রিভুজ বলে। যেমন-
চিত্রে ∠B = ৯০ ডিগ্রি বা ১ সমকোণ

সমকোণী ত্রিভুজের বৈশিষ্ট্যঃ

সমকোণী ত্রিভুজের একটি কোণ অবশ্যই এক সমকোণ বা ৯০ ডিগ্রি হতে হবে।
সমকোণের বিপরীত বাহুকে অতিভুজ বলা হয়।
সমকোণী ত্রিভুজের অতিভুজ ই বৃহত্তম বাহু ।
সমকোণ ব্যতীত অন্য দুটি কোণ সূক্ষ্মকোণ এবং এরা পরস্পরের পূরক (কারণ যোগফল ৯০°)
সমকোণ সংলগ্ন বাহুদ্বয়ের যে কোন একটিকে লম্ব এবং অপরটিকে ভূমি ধরা যায়। (অর্থাৎ লম্ব ও ভূমি নির্দিষ্ট নয়।)
সমকোণী ত্রিভুজের সমকোণ সংলগ্ন বাহুদ্বয়ের উপর অংকিত বর্গক্ষেত্রদ্বয়ের ক্ষেত্রফলের সমষ্টি অপর বাহুর উপর অংকিত বর্গক্ষেত্রের ক্ষেত্রফলের সমান। এটা পীথাগোরাসের উপপাদ্য নামে পরিচিত যাকে লেখা যায়, ${AC}^{2} = {AB}^{2} + {BC}^{2} ({অতিভূজ}^{2} = {লম্ব}^{2} + {ভূমি}^{2})$
সমকোণী ত্রিভুজ

• বাহুর মাধ্যমে চেনার উপায়:

ক্ষুদ্রতম দুই বাহুর বর্গের সমষ্টি উহার বৃহত্তর বাহুর বর্গের সমান হলে তা সমকোণী ত্রিভুজ হয়।

সমকোণী ত্রিভুজের ক্ষেত্রফল = $\frac{১}{২}$ × ভূমি × উচ্চতা

[ এই সূত্রটি শুধু সমকোণী ত্রিভুজে কাজে লাগবে বিষয়টা এমন নয় বরং যেখানে ভূমি ও উচ্চতার মান দেয়া থাকবে সেখানেই এই সূত্রটি প্রয়োগ করে সমাধান করা যাবে। ]

পীথাগোরাসের উপপাদ্য:

সমকোণী ত্রিভুজের অতিভুজের উপর অংকিত বর্গক্ষেত্র , ঐ ত্রিভুজের অপর দুই বাহুর উপর অংকিত বর্গক্ষেত্রের সমষ্টির সমান।
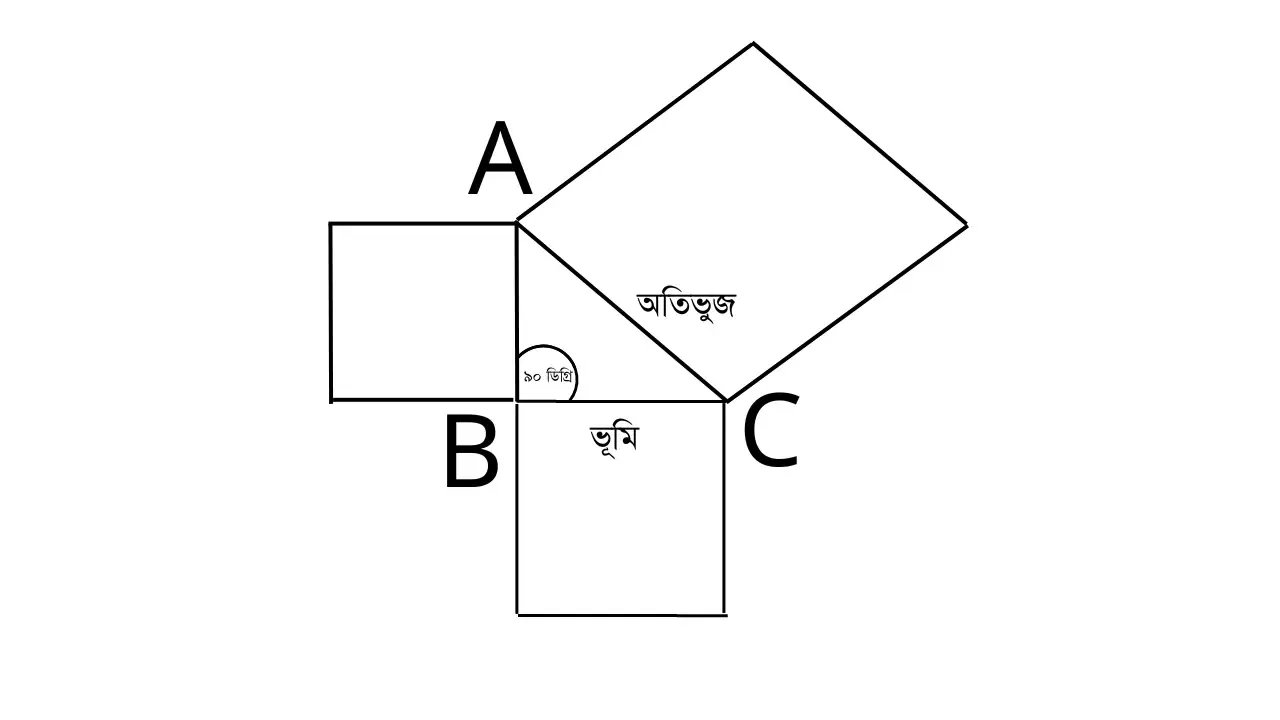পীথাগোরাসের উপপাদ্য ব্যাখ্যা: এখানে ABC ত্রিভুজের প্রতিটি বাহুর উপর একটি করে বর্গক্ষেত্র তৈরী করা হয়েছে । যার মধ্যে অতিভুজ AC বাহুর অংকিত বর্গক্ষেত্রটি AB এবং AC বাহুদ্বয়ের উপর অংকিত বর্গক্ষেত্রদ্বয়ের সমষ্টির সমান । এই কথাটিই পীথাগোরাসের সূত্রানুসারে এভাবে লিখতে হয়, ${AC}^{2} = {AB}^{2} + {BC}^{2}$
চিত্রানুসারে AC = 5 , AB = 3 এবং BC = 4
সূত্রে মানগুলো বসিয়ে পাই , $5^{2} = 3^{2} + 4^{2}$
বা, 25 = 9 + 16
বা, 25 = 25

এখন, অতিভুজ AC = 5 এর পরিবর্তে ৬ ধরলে মানগুলো পূর্ণ সংখ্যায় মিলবে না , তাই কখনো লম্ব ও ভূমি ৩ ও ৪ মিটার হলে অতিভুজ অবশ্যই ৫ মিটার হবে ।

এই সূত্রটি দিয়ে পরবর্তীতে প্রচুর প্রশ্ন সমাধান করা যাবে । তাই গুরুত্ব দিয়ে বুঝুন ।

সূক্ষ্মকোণী ত্রিভুজ (Acute Angled Triangle):

যে ত্রিভুজের তিনটি কোণ সূক্ষ্মকোণ (৯০ ডিগ্রি এর থেকে কম) তাকে সূক্ষ্মকোণী ত্রিভুজ বলে। যেমন-
চিত্রে △ABC একটি সূক্ষ্মকোণী ত্রিভুজ।

সূক্ষকোণী ত্রিভূজের বৈশিষ্ট্য:

সূক্ষকোণী ত্রিভূজের তিনটি কোণই সূক্ষকোণ অর্থাৎ ৯০ ডিগ্রি এর থেকে কম ।
সমবাহু ত্রিভূজ একটি সূক্ষকোণী ত্রিভূজ যার প্রতিটি কোণ ৬০ ডিগ্রি ।
সূক্ষকোণী ত্রিভূজের যে কোন দুই বাহুর বর্গের সমষ্টি অপর বাহুর বর্গের চেয়ে বৃহত্তর ।

স্থূলকোণী ত্রিভুজ (Obtuse Angled Triangle) :

যে ত্রিভুজের একটি কোণ স্থূলকোণ তাকে স্থূলকোণী ত্রিভুজ বলে। যেমন-
চিত্রে △ABC একটি স্থূলকোণী ত্রিভুজ কারণ ∠B স্থূলকোণ ।

স্থূলকোণী ত্রিভূজের বৈশিষ্ট্য:

স্থূলকোণী ত্রিভূজের একটি কোণ স্থূলকোণ এবং অন্য দুটি কোণ সূক্ষ্মকোণ ।
বৃহত্তম বাহুর বর্গ অপর দুই বাহুর বর্গের সমষ্টির চেয়ে বৃহত্তর ।

সমবাহু ত্রিভুজ (Equilateral Triangle):

যে ত্রিভুজের তিনটি বাহুই পরস্পর সমান তাঁকে সমবাহু ত্রিভুজ বলে। যেমন-
যেমন △ABC একটি সমবাহু ত্রিভুজ যার প্রতিটি বাহু পরস্পর সমান এবং প্রত্যেকটি কোণ ৬০ ডিগ্রি ।

সমবাহু ত্রিভুজের বৈশিষ্ট্য:

তিনটি বাহু সমান ।
কোণ তিনটি ও সমান।
প্রত্যেক কোণের পরিমান ৬০ ডিগ্রি । যেহেতু তিন বাহু সমান তাই কোণগুলোও সমান হবে। আবার তিনটি কোণের সমষ্টি ১৮০ ডিগ্রি, তাই একটি কোণ হবে ১৮০÷৩ = ৬০ ডিগ্রি
শুধু পরিসীমা দেয়া থাকলে একমাত্র সমবাহু ত্রিভুজ আঁকা সম্ভব ।
সমবাহু ত্রিভুজকে সূক্ষকোণী ত্রিভুজ ও বলা যায় কারণ সমবাহু ত্রিভুজের প্রতিটি কোণই সূক্ষকোণ ।

সমবাহু ত্রিভুজের সুত্র:

△সমবাহু ত্রিভুজের পরিসীমা: এক বাহু a হলে, পরিসীমা = 3a ( ত্রিভুজের 3 বাহুর যোগফল) ।
△সমবাহু ত্রিভুজের ক্ষেত্রফল = $\frac{√3}{4} a^{2}$ (সমবাহু ত্রিভুজের এক বাহুর দৈর্ঘ্য a হলে)

সমদ্বিবাহু ত্রিভুজ (Isosceles Triangle):

যে ত্রিভুজের দু’টি বাহু সমান তাকে সমদ্বিবাহু ত্রিভুজ বলে । যেমন-
চিত্রে △ABC একটি সমদ্বিবাহু ত্রিভুজ । যার AB বাহু = AC বাহু ।

সমদ্বিবাহু ত্রিভুজের বৈশিষ্ট্য:

দুটি বাহু পরস্পর সমান। চিত্রে AB = AC .
সমান সমান বাহুর বিপরীত কোণদ্বয় ও সমান ।
সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফল = $\frac{b}{4} \sqrt{4 a^{2} - b^{2}}$ ( যেখানে b = ভূমি এবং a = সমান সমান বাহুদ্বয়ের দৈর্ঘ্য )

বিষমবাহু ত্রিভুজ (Scalene Triangle):

যে ত্রিভুজের তিনটি বাহুই অসমান তাকে বিষমবাহু বা অসমবাহু ত্রিভুজ বলে । যেমন-
চিত্র: বিষমবাহু ত্রিভুজ

বিষমবাহু ত্রিভুজের বৈশিষ্ট্য:

প্রতিটি বাহু অসমান
মধ্যমাগুলো অসমান
বিষমবাহু ত্রিভুজের ক্ষেত্রফল = $\sqrt{s(s - a ) ( s - b ) ( s - c )}$
এখানে 2S ( পরিসীমা ) = a + b + c
সুতরাং S ( অর্ধ পরিসীমা ) = $\frac{a + b + c}{2}$

বিভিন্ন প্রতিযোগিতামূলক পরীক্ষার প্রশ্ন ও সমাধান

১. ১৭ সে.মি., ১৫ সে.মি., ৮ সে.মি. বাহু বিশিষ্ট ত্রিভুজটি হবে- [ কারা তত্ত্বাবধায়ক-২০১৯]

(ক) সমবাহু (খ) সমদ্বিবাহু (গ) সমকোণী (ঘ) স্থূলকোণী

উত্তরঃ (গ) সমকোণী

Explanation:
ত্রিভুজটি সমকোণী কারণ এর অতিভুজ ১৭ কে বর্গ করলে ২৮৯ হয়।আবার ভূমি এবং উচ্চতা যথাক্রমে ১৫ ও ৮ এর বর্গের সমষ্টি ২৮৯ হয়। অর্থাৎ ${(অতিভুজ)}^{২} = {(লম্ব)}^{২} + {(ভূমি)}^{২}$ হয় ।যা সমকোণী ত্রিভুজের ক্ষেত্রে প্রযোজ্য।

২. ΔABC এ ∠A = ৪০ ডিগ্রি, ∠B = ৭০ ডিগ্রি, হলে ΔABC কি ধরনের ত্রিভুজ? [সাব রেজিস্ট্রার-২০০১]

(ক) সমকোণী (খ) স্থুলকোণী (গ) সমদ্বিবাহু (ঘ) সমবাহু

উত্তরঃ (গ) সমদ্বিবাহু

Explanation:
আমরা জানি, ত্রিভুজের তিনকোণের সমষ্টি = ১৮০ ডিগ্রি
দেওয়া আছে , ∠A = ৪০ ডিগ্রি, ∠B = ৭০ ডিগ্রি
তাহলে তৃতীয় কোণ ∠C = ১৮০ - (∠A+∠B)
= ১৮০ -(৪০+৭০)
= ১৮০- ১১০
= ৭০ ডিগ্রি
দেখা যাচ্ছে , ∠B এবং ∠C সমান।তাই দুটি বাহু ও সমান।অতএব,ত্রিভুজটি সমদ্বিবাহু।

৩.যদি সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য a হয়,তবে ক্ষেত্রফল কত হবে? [ প্রাক প্রাথমিক সহকারী শিক্ষক(ভলগা)-২০১৩]

(ক)

\frac{√৩}{৪} a^{২}

(খ)

\frac{√৩}{২} a^{২}

(গ)

\frac{৩}{২} a^{২}

(ঘ)

\frac{১}{২} a^{২}

উত্তরঃ (ক) $\frac{√৩}{৪} a^{২}$

Explanation:
সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য a হলে ক্ষেত্রফল $\frac{√৩}{৪} a^{২}$ ।এটা সূত্র।

৪. কোন ত্রিভুজের একটি বাহু উভয় দিকে বর্ধিত করায় উৎপন্ন বহিঃস্থ কোণগুলি পরস্পর সমান হলে ত্রিভুজটি---- [রেজিঃ বেসরকারি প্রাথমিক সহকারী শিক্ষক-২০১১(টগর)]

(ক) বিষমবাহু (খ) সমদ্বিবাহু (গ) সমবাহু (ঘ) সমকোণী

উত্তরঃ (খ) সমদ্বিবাহু

Explanation:
ত্রিভুজের অন্তঃস্থ কোণ ও বহিঃস্থ কোণের সমষ্টি দুই সমকোণ।সুতরাং ত্রিভুজের দুটি বহিঃস্থ কোণ সমান হলে ত্রিভুজটির অন্তঃস্থ কোণ দুটি ও সমান হবে। অর্থাৎ ত্রিভুজটি সমদ্বিবাহু হবে।

৫. একটি সমকোণী ত্রিভুজের সমকোণ ছাড়া অন্য দুটি কি কোণ? [ রেজিঃ বেসরকারি প্রাথমিক সহকারী শিক্ষক-২০১১(টগর)]

(ক) সন্নিহিত কোণ (খ) সরল কোণ (গ) সূক্ষ্মকোণ (ঘ) পূরক কোণ

উত্তরঃ (গ) সূক্ষ্মকোণ

Explanation:
যেহেতু ত্রিভুজের তিন কোণের সমষ্টি = ১৮০ ডিগ্রি । তাই এক সমকোণ = ৯০ ডিগ্রি বাদ দিলে থাকবে ৯০ ডিগ্রি । এই ৯০ ডিগ্রি যদি অপর দুটি কোণের সমষ্টি হয় তাহলে কোণ দুইটির প্রত্যেকটি অবশ্যই ৯০ ডিগ্রি এর চেয়ে ছোট হবে । ৯০ ডিগ্রি এর চেয়ে ছোট কোণকে সূক্ষ্মকোণ বলে।তাই একটি সমকোণী ত্রিভুজের সমকোণ ছাড়া অন্য দুটি কোণ সূক্ষ্মকোণ হবে।

৬. কোনো ত্রিভুজের তিন কোণের দ্বিখন্ডকগুলো যে বিন্দুতে ছেদ করে তাকে কি বলে? [ ১৪তম বিসিএস]

(ক) বহিঃকেন্দ্র (খ) ভরকেন্দ্র (গ) পরিকেন্দ্র (ঘ) অন্তঃকেন্দ্র

উত্তরঃ (ঘ) অন্তঃকেন্দ্র

Explanation:
লম্ববিন্দু: ত্রিভুজের তিনটি শীর্ষ থেকে বিপরীত বাহুর উপর অঙ্কিত লম্ব যে বিন্দুতে মিলিত হয় তাকে লম্ববিন্দু বলে।
লম্বদুরত্ব: লম্ববিন্দু থেকে ত্রিভুজের শীর্ষ বিন্দুর দুরত্বকে লম্বদুরত্ব বলে।
ভরকেন্দ্র: ত্রিভুজের মধ্যমাত্রয় যে বিন্দুতে মিলিত হয় তাকে ভরকেন্দ্র বলে।
পরিকেন্দ্র: ত্রিভুজের যেকোনো দুই বাহুর সমদ্বিখন্ডকদ্বয় যে বিন্দুতে মিলিত হয় তাকে পরিকেন্দ্র বলে।
পরিব্যাসার্ধ: পরিকেন্দ্র থেকে ত্রিভুজের শীর্ষ বিন্দুর দুরত্বকে পরিব্যাসার্ধ বলে।
অন্তঃকেন্দ্র : ত্রিভুজের তিনটি কোণের সমদ্বিখন্ডকত্রয় যে বিন্দুতে মিলিত হয় তাকে অন্তঃকেন্দ্র বলে।
বহিঃকেন্দ্র: ত্রিভুজের একটি কোণের অন্ত-সমদ্বিখন্ডক এবং অপর দুই কোণের বহি-সমদ্বিখন্ডক যে বিন্দুতে মিলিত হয় তাকে বহিঃকেন্দ্র বলে।
নব-বিন্দুর কেন্দ্র : ত্রিভুজের নয়টি মূল বিন্দুগামী বৃত্তের কেন্দ্র হল নয়-বিন্দুর কেন্দ্র বা নববিন্দু কেন্দ্র।

৭. ABC একটি সমদ্বিবাহু ত্রিভুজ। ∠A শীর্ষ কোণ। ∠B ও ∠C দুটি ভূমি কোণ। AB বাহু = AC বাহু। ∠B = ৭৫ ডিগ্রি । ∠A = কত ডিগ্রী? [২৬ তম বিসিএস]

(ক) ২৫ ডিগ্রি (খ) ৩০ ডিগ্রি (গ) ৬০ ডিগ্রি (ঘ) ৫০ ডিগ্রি

উত্তরঃ (খ) ৩০ ডিগ্রি

Explanation:
যেহেতু ABC একটি সমদ্বিবাহু ত্রিভুজ।তাহলে বাহু দুইটি যদি সমান হয় তবে দুটি ভূমি কোণ ∠B ও ∠C সমান হবে। ভূমি ∠B = ৭৫ ডিগ্রী হলে , ∠C= ৭৫ ডিগ্রী । দুটি ভূমি কোণ ∠B ও ∠C মিলে ৭৫ ডিগ্রী +৭৫ ডিগ্রী = ১৫০ ডিগ্রী ।যেহেতু ত্রিভুজের তিন কোণের সমষ্টি ১৮০ ডিগ্রী ।তাই অবশিষ্ট শীর্ষ কোণ ∠A = ১৮০ - ১৫০ = ৩০ ডিগ্রী ।

৮. একটি সমকোণী ত্রিভুজের ভূমি ৮ ফুট এবং লম্ব ৬ ফুট হলে অতিভুজের দৈর্ঘ্য কত? [২৭ তম বিসিএস]

(ক) ৯ ফুট (খ) ১০ ফুট (গ) ১১ ফুট (ঘ) ১২ ফুট

উত্তরঃ (খ) ১০ ফুট

Explanation:
আমরা জানি, সমকোণী ত্রিভুজের
${(অতিভুজ)}^{২} = {(ভুমি)}^{২} + {(লম্ব)}^{২}$
বা, ${(অতিভুজ)}^{২} = ৮^{২} + ৬^{২}$
বা, ${(অতিভুজ)}^{২} = ৬৪ + ৩৬$
বা, ${(অতিভুজ)}^{২} = ১০০$
সুতরাং অতিভুজ = ১০ [ বর্গমূল করে]

৯. ⊿ABC- এর BC বাহুকে D পর্যন্ত বাড়ানো হল। ∠A = ৬০ ডিগ্রি এবং ∠B = ৯০ ডিগ্রি হলে, ∠ACD = কত? [ ৪০ তম বিসিএস]

(ক) ৯০ ডিগ্রি (খ) ১৫০ ডিগ্রি (গ) ১৬০ ডিগ্রি (ঘ) ১৭০ ডিগ্রি

উত্তরঃ (খ) ১৫০ ডিগ্রি

Explanation:
দেওয়া আছে , ∠A = ৬০ ডিগ্রি এবং ∠B = ৯০ ডিগ্রি । তাহলে ∠C = ১৮০-(৬০+৯০)=১৮০-১৫০ = ৩০ ডিগ্রি । BC বাহুকে D পর্যন্ত বাড়ানো হলে BCD একটি সরল কোণ উৎপন্ন হয়।এক সরলকোণ = ১৮০ ডিগ্রি । এই সরলকোণের একপাশের কোণ ∠C বা ∠BCA = ৩০ ডিগ্রি । তাহলে অপর পাশের কোণ ∠ACD = ১৮০-৩০ = ১৫০ ডিগ্রি ।

১০. কোন ত্রিভুজের কোণত্রয়ের সমদ্বিখন্ডকের ছেদবিন্দুকে কি বলে? [ শ্রম অধিদপ্তর-২০১৩]

(ক) ভরকেন্দ্র (খ) পরিকেন্দ্র (গ) বহিঃকেন্দ্র (ঘ) অন্তঃকেন্দ্র

উত্তরঃ (ঘ) অন্তঃকেন্দ্র

১১. কোন ত্রিভুজের দুটি কোণ ১০ ডিগ্রি ও ৮০ ডিগ্রি । ত্রিভুজটি-- [স্বরাষ্ট্র মন্ত্রণালয়ের প্রশাসনিক কর্মকর্তা-২০১৩]

(ক) সমকোণী (খ) স্থূলকোণী (গ) সূক্ষ্মকোণী (ঘ) বলা সম্ভব নয়

উত্তরঃ (ক) সমকোণী

Explanation:
দেওয়া আছে , দুটি কোণ ১০ ডিগ্রি ও ৮০ ডিগ্রি ।এদের সমষ্টি = ১০ + ৮০ = ৯০ ডিগ্রি । যেহেতু ত্রিভুজের তিনকোণের সমষ্টি ১৮০ ডিগ্রি ।তাই অপর কোণটি অবশ্যই ৯০ ডিগ্রি হবে।যেহেতু একটি ৯০ ডিগ্রি হয় তাহলে ত্রিভুজটি অবশ্যই সমকোণী ত্রিভুজ।

১২. ত্রিভুজের ক্ষেত্রফল - [ অগ্রণী ব্যাংক অফিসার-২০০৮]

(ক)

\frac{১}{২}

( ভূমি × উচ্চতা) (খ)

\frac{১}{২}

( ভূমি ÷ উচ্চতা) (গ)

\frac{১}{২}

( ভূমি + উচ্চতা) (ঘ)

\frac{১}{২}

( ভূমি - উচ্চতা)

উত্তরঃ (ক) $\frac{১}{২}$ ( ভূমি × উচ্চতা)

১৩. একটি সমদ্বিবাহু সমকোণী ত্রিভুজের অতিভুজের দৈর্ঘ্য ১২ সেমি হলে, ত্রিভুজটির ক্ষেত্রফল কত বর্গ সেমি? [এনএসআই-২০০৮]

(ক) ৩৬ (খ) ৪৮ (গ) ৫৬ (ঘ) ৭২

উত্তরঃ (ক) ৩৬

Explanation:
সমান সমান বাহুর দৈর্ঘ্য a হলে,
$a^{2} + a^{2} = 12^{2}$
বা, ${2a}^{2} = 144$
বা, $a^{2} = 72$
ত্রিভুজটির ক্ষেত্রফল = $\frac{1}{2} \times a \times a$
= $\frac{1}{2} \times a^{2}$
= $\frac{1}{2} \times 72$
= 36

১৪. ABC ত্রিভুজের B কোণটি C কোণের সমান, D হচ্ছে BC বাহুর মধ্য একটি বিন্দু। নিচের কোন বক্তব্যটি সঠিক? [ থানা শিক্ষা অফিসার-১৯৯৯]

(ক) AB > BC (খ) AB < BC (গ) BD > CD (ঘ) AC > AD

উত্তরঃ (ঘ) AC > AD

১৫. ত্রিভুজের যে কোন দুটি মধ্যমা পরস্পর সমান হলে ত্রিভুজটি? [প্রধানমন্ত্রীর কার্যালয়ের সহকারী পরিচালক-২০০৮]

(ক) সমবাহু ত্রিভুজ (খ) সমদ্বিবাহু ত্রিভুজ (গ) বিষমবাহু ত্রিভুজ (ঘ) সমকোণী ত্রিভুজ

উত্তরঃ (খ) সমদ্বিবাহু ত্রিভুজ

Explanation:
ত্রিভুজের যে কোন দুটি মধ্যমা পরস্পর সমান হলে ত্রিভুজটি সমদ্বিবাহু হয় এবং ত্রিভুজের তিনটি মধ্যমা পরস্পর সমান হলে ত্রিভুজটি সমবাহু হয়।

১৬. একটি সমকোণী ত্রিভুজের ভূমির দৈর্ঘ্য লম্ব অপেক্ষা ১ মিটার কম এবং লম্ব অপেক্ষা অতিভুজের দৈর্ঘ্য ১ মিটার বেশি হলে উহার অতিভুজের দৈর্ঘ্য কত ? [বাংলাদেশ ব্যাংক সহকারী পরিচালক-২০০৮]

(ক) ৪ মি (খ) ৩ মি (গ) ৬ মি (ঘ) ৫ মি

উত্তরঃ (ঘ) ৫ মি

Explanation:
ধরি, লম্ব = x মি।
∴ভূমি = (x + 1) মিটার
∴ অতিভুজ = (x + 2) মিটার
∴ ABC সমকোণী ত্রিভুজ বলে,
বা, ${(x + 2)}^{2} = x^{2} + {(x + 1)}^{2}$
বা, $x^{2} + 4x + 4 = x^{2} + x^{2} + 2x + 1$
বা, $x^{2} - 2x - 3 = 0$
বা, $x^{2} - 3x + x - 3 = 0$
বা, x (x - 3) + 1(x - 3) = 0
বা, (x - 3) (x + 1) = 0
বা, x - 3 = 0
∴ x = 3

অথবা,
x + 1 = 0
∴ x = ⁻1
∴x ≠ ⁻1
∴ x = 3
∴ অতিভুজ = 3 + 2 = 5 মিটার

১৭. কোন ত্রিভুজের বাহুগুলোর অনুপাত নিচের কোনটি হলে একটি সমকোণী ত্রিভুজ অঙ্কন সম্ভব হবে? [ অগ্রণী ব্যাংক অফিসার-২০০৬]

(ক) ৬ : ৫ : ৪ (খ) ৩ : ৪ : ৫ (গ) ১২ : ৮ : ৪ (ঘ) ৬ : ৪ : ৩

উত্তরঃ (খ) ৩ : ৪ : ৫

Explanation:
সমকোণী ত্রিভুজ হতে হলে, ${(অতিভুজ)}^{২} = {(ভুমি)}^{২} + {(লম্ব)}^{২}$ হতে হবে।এখানে যদি অপশনভিত্তিক যাচাই করা হয় তাহলে খ ই সঠিক উত্তর।এখানে ৫ অতিভুজ ধরলে $৫^{২}$ সমান $৩^{২}$ ও $৪^{২}$ এর যোগফল হবে।

১৮. একটি সমবাহু ত্রিভুজের একটি বাহু ১৬ মিটার। ত্রিভুজটির ক্ষেত্রফল কত? [প্রাক প্রাথমিক সহকারী শিক্ষক(গামা)-২০১৪]

(ক) ৬৪√৩ (খ) ১৯২ (গ) ৬৪ (ঘ) ৩২√৩

উত্তরঃ (ক) ৬৪√৩

Explanation:
ধরি , সমবাহু ত্রিভুজের বাহুর দৈঘ্য = a
তাহলে , সমবাহু ত্রিভুজের ক্ষেত্রফল = $\frac{√৩}{৪} a^{২}$
= $\frac{√৩}{৪} {(১৬)}^{২}$
= $\frac{√৩}{৪} \times ২৫৬$
= ৬৪√৩

১৯. অতিভূজের বিপরীতে থাকে-- [ প্রাক প্রাথমিক সহকারী-২০১৩]

(ক) সমকোণ (খ) সরলকোণ (গ) স্থুলকোণ (ঘ) সূক্ষ্মকোণ

উত্তরঃ (ক) সমকোণ

২০. একটি সমবাহু ত্রিভুজের এক বাহুর দৈর্ঘ্য ৪ সে : মি : হলে, উহার ক্ষেত্রফল হবে কত? [ পরিবার পরিকল্পনা কমকতা-২০০৯]

(ক) √৩ বর্গ সেঃ মিঃ (খ) ২√৩ বর্গ সেঃ মিঃ (গ) ৪√৩ বর্গ সেঃ মিঃ (ঘ) ১২ √৩ বর্গ সেঃ মিঃ

উত্তরঃ (গ) ৪√৩ বর্গ সেঃ মিঃ

Explanation:
ধরি , সমবাহু ত্রিভুজের বাহুর দৈঘ্য = a
তাহলে , সমবাহু ত্রিভুজের ক্ষেত্রফল = $\frac{√৩}{৪} a^{২}$
= $\frac{√৩}{৪} {(৪)}^{২}$
= $\frac{√৩}{৪} \times ১৬$
= ৪√৩

২১. একটি কোণের মান তার পূরক কোণের মানের অর্ধেকের সমান। কোণটির মান কত? [ প্রাথমিক সহকারী শিক্ষক-২০১২]

(ক) ২৫ ডিগ্রি (খ) ৬০ ডিগ্রি (গ) ৪৫ ডিগ্রি (ঘ) ৩০ ডিগ্রি

উত্তরঃ (ঘ) ৩০ ডিগ্রি

Explanation:
আমরা জানি, দুইটি সন্নিহিত কোণের সমষ্টি ১ সমকোণ বা ৯০ ডিগ্রি হলে একটিকে অপরটির পূরক কোণ বলে।ধরা যাক, কোণটির মান ৩০ ডিগ্রি । তাহলে তার পূরক কোণ ৬০ ডিগ্রি ।৩০ ডিগ্রি এই ৬০ ডিগ্রি এর সমান।এভাবে অপশনভিত্তিক যাচাই করাটাই সবচেয়ে বেশি সুৃবিধা এবং সহজ হবে।

২২. সমদ্বিবাহু ত্রিভুজের সমান বাহুদ্বয় বর্ধিত করলে উৎপন্ন কোণদ্বয় হবে-- [প্রাক প্রাথমিক সহকারী শিক্ষক(গামা)-২০১৪]

(ক) সূক্ষ্মকোণ (খ) স্থুলকোণ (গ) সরলকোণ (ঘ) সমকোণ

উত্তরঃ (খ) স্থুলকোণ

Explanation:
ধরা যাক, ABC ত্রিভুজের ABC = AC বাহু।বাহুদ্বয়কে যথাক্রমে E ও F পর্যন্ত বর্ধিত করা হলো।উৎপন্ন বহিঃস্থ কোণদ্বয় ∠EBC ও ∠FCB যা একসমকোণ অপেক্ষা বড়। সুতরাং ∠EBC ও ∠FCB স্থুলকোণ।

২৩. একটি ত্রিভুজের তিনটি বাহুর দৈর্ঘ্য ৫, ৬, ৭ মিটার। নিকটতম বর্গমিটারে ত্রিভুজটির ক্ষেত্রফল কত? [স্বাস্থ্য সহকারী-২০১০]

(ক) ১৬ বর্গমিটার (খ) ১৫ বর্গমিটার (গ) ১৭ বর্গমিটার (ঘ) ১৪ বর্গমিটার

উত্তরঃ (খ) ১৫ বর্গমিটার

Explanation:
বিষমবাহু ত্রিভুজের পরিসীমা 2s = ৫ + ৬ + ৭ = ১৮ মিটার
সুতরাং অর্ধ পরিসীমা S = ১৮ ÷ ২ = ৯ মিটার
বিষমবাহু ত্রিভুজের পরিসীমা 2s হলে ক্ষেত্রফল = $\sqrt{s(s - a ) ( s - b ) ( s - c )}$
= $\sqrt{৯(৯ - ৫ ) ( ৯ - ৬ ) ( ৯ - ৭ )}$
= $\sqrt{৯×৪×৩×২}$
= $\sqrt{২১৬}$
= ১৪.৬৯
যা নিকটতম বর্গমিটারে ১৫ বর্গমিটার

২৪. ত্রিভুজের শীর্ষবিন্দু থেকে এর ভূমির উপর অঙ্কিত লম্বের দৈর্ঘ্য কে কি বলা হয়? [ প্রাক প্রাথমিক সহকারী শিক্ষক(২৭.০৬.২০১৫)]

(ক) মধ্যমা (খ) কর্ণ (গ) অতিভুজ (ঘ) উচ্চতা

উত্তরঃ (ঘ) উচ্চতা

Explanation:
ত্রিভুজের শীর্ষবিন্দু থেকে এর ভূমির উপর অঙ্কিত লম্বের দৈর্ঘ্য কে উচ্চতা বলা হয়।

২৫. একটি সমবাহু ত্রিভুজের ক্ষেত্রফল ৫০ বর্গ সেঃ মিঃ। ত্রিভুজের প্রতি বাহুর দৈর্ঘ্য কত? [পরিবার কল্যাণ পরিদর্শক-২০০১]

(ক) ১৫.২ সেঃ মিঃ (খ) ১০.৫ সেঃ মিঃ (গ) ১০.৭ সেঃ মিঃ (ঘ) ১৭.১ সেঃ মিঃ

উত্তরঃ (গ) ১০.৭ সেঃ মিঃ

Explanation:
ধরি , সমবাহু ত্রিভুজের বাহুর দৈঘ্য = a
তাহলে , সমবাহু ত্রিভুজের ক্ষেত্রফল = $\frac{√৩}{৪} a^{২}$
প্রশ্নমতে, $\frac{√৩}{৪} a^{২}$ = ৫০ বর্গ সেঃ মিঃ
বা, $\frac{√৩}{৪} a^{২} \times ৪$ = ৫০ × ৪
বা, $√৩ a^{২}$ = ২০০
বা, $a^{২} = \frac{২০০}{√৩}$
বা, $a^{২} = ১১৫.৪৭$
বা, a = ১০.৭ [ বর্গমূল করে ]
সুতরাং ত্রিভুজের প্রতি বাহুর দৈর্ঘ্য = ১০.৭ সেমি

২৬. একটি সমকোণী ত্রিভুজের দ্বিতীয় কোণটির মাপ ২০ ডিগ্রি হলে তৃতীয় কোণটির মাপ-- [ প্রাক প্রাথমিক সহকারী শিক্ষক-২০১৩]

(ক) ৪০ ডিগ্রি (খ) ৫০ ডিগ্রি (গ) ৬০ ডিগ্রি (ঘ) ৭০ ডিগ্রি

উত্তরঃ (ঘ) ৭০ ডিগ্রি

Explanation:
আমরা জানি ,ত্রিভুজের তিন কোণের সমষ্টি ১৮০ ডিগ্রি এবং সমকোণী ত্রিভুজের একটি কোণ অবশ্যই ৯০ ডিগ্রি ।বাকি থাকল ৯০ ডিগ্রি । এর মধ্যে একটি কোণ ৯০ ডিগ্রি হলে অপর কোণটি অবশ্যই ৯০ - ২০ = ৭০ ডিগ্রি।

২৭. ABC ত্রিভুজে AB = AC , ∠A = ৮০ ডিগ্রি , ∠B = কত? [ সাব রেজিঃ -২০০১]

(ক) ৪০ ডিগ্রি (খ) ৫০ ডিগ্রি (গ) ৬০ ডিগ্রি (ঘ) ১০০ ডিগ্রি

উত্তরঃ (খ) ৫০ ডিগ্রি

Explanation:
ত্রিভুজটি সমদ্বিবাহু তাই এর দুৃটি কোণ অবশ্যই সমান হবে। এখানে একটি কোণ ৮০ ডিগ্রি হলে অপর দুটি কোণ অবশ্যই ৫০ ডিগ্রি করে হবে।যেহেতু তিন কোণের সমষ্টি ১৮০ ডিগ্রি ।

২৮. একটি সমকোণী সমদ্বিবাহু ত্রিভুজের তিন কোণের পরিমাণ--- [তথ্য সহকারী-২০১৩]

(ক) ৬০ ডিগ্রি, ৬০ ডিগ্রি, ৬০ ডিগ্রি (খ) ৪০ ডিগ্রি, ৯০ ডিগ্রি, ৪০ ডিগ্রি (গ) ৫০ ডিগ্রি, ৯০ ডিগ্রি, ৪০ ডিগ্রি (ঘ) ৪৫ ডিগ্রি, ৯০ ডিগ্রি, ৪৫ ডিগ্রি

উত্তরঃ (ঘ) ৪৫ ডিগ্রি, ৯০ ডিগ্রি, ৪৫ ডিগ্রি

Explanation:
সমকোণী সমদ্বিবাহু ত্রিভুজ।তার মানে একটি কোণ এক সমকোণ বা ৯০ ডিগ্রি এবং অপর দুটি কোণ সমান। অপর দুটি কোণ সমান হলে ৯০ ডিগ্রি কে দুই ভাগে ভাগ করতে হবে।তাই অপর দুটি কোণের প্রত্যেকটি হবে ৪৫ ডিগ্রি ।

২৯. কোন ত্রিভুজের এক বাহুর উপর অঙ্কিত বর্গক্ষেত্র অপর দুই বাহুর উপর অঙ্কিত বর্গক্ষেত্রদ্বয়ের যোগফলের সমান হলে ত্রিভুজটি হবে-- ...

(ক) সমকোণী (খ) সূক্ষ্মকোণী (গ) সমবাহু (ঘ) স্থূলকোণী

উত্তরঃ (ক) সমকোণী

Explanation:
পীথাগোরাসের উপপাদ্য অনুসারে, সমকোণী ত্রিভুজের এক বাহুর উপর অঙ্কিত বর্গক্ষেত্র অপর দুই বাহুর উপর অঙ্কিত বর্গক্ষেত্রদ্বয়ের সমষ্টির সমান ।

৩০. সমবাহু ত্রিভুজের প্রত্যেকটি কোণের পরিমাণ কত? [ বাণিজ্য সহকারী পরিচালক-২০১৩]

(ক) ৬০ ডিগ্রি (খ) ৯০ ডিগ্রি (গ) ১৮০ ডিগ্রি (ঘ) ৩৬০ ডিগ্রি

উত্তরঃ (ক) ৬০ ডিগ্রি

Explanation:
সমবাহু ত্রিভুজের প্রত্যেকটি কোণের পরিমাণ ৬০ ডিগ্রি এবং প্রতিটি বাহু পরস্পর সমান ।

৩১. যে ত্রিভুজের দুটি বাহু পরস্পর সমান, তা--- [ মাদক অধিদপ্তর -২০১৩]

(ক) সমদ্বিবাহু ত্রিভুজ (খ) সমবাহু ত্রিভুজ (গ) বিষমবাহু ত্রিভুজ (ঘ) বিপরীত বাহু ত্রিভুজ

উত্তরঃ (ক) সমদ্বিবাহু ত্রিভুজ

Explanation:
যে ত্রিভুজের দুটি বাহু পরস্পর সমান, তাকে সমদ্বিবাহু ত্রিভুজ বলে ।

৩২. কোনো ত্রিভুজের একটি কোণ অপর দুটি কোণের সমান হলে ত্রিভুজটি --- [ খাদ্য অধিদপ্তর পরিদর্শক-২০১২]

(ক) সমবাহু (খ) সমকোণী (গ) সূক্ষ্মকোণী (ঘ) স্থুলকোণী

উত্তরঃ (খ) সমকোণী

৩৩. কোন ত্রিভুজের তিন বাহুর সমদ্বিখন্ডকগুলোর ছেদবিন্দুর নাম কি? [ প্রাথমিক প্রধান শিক্ষক-২০১২(ক্যামেলিয়া)]

(ক) বহিঃকেন্দ্র (খ) অন্তঃকেন্দ্র (গ) ভরকেন্দ্র (ঘ) পরিকেন্দ্র

উত্তরঃ (গ) ভরকেন্দ্র

৩৪. একটি সমদ্বিবাহু ত্রিভুজের একটি কোণের পরিমাণ ৫০ ডিগ্রি হলে অপর দুটি কোণের প্রত্যেকটির পরিমাণ হবে-- [সহকারী আবহাওয়াবিদ-২০০০]

(ক) ৫৫ ডিগ্রি (খ) ৭৫ ডিগ্রি (গ) ৬০ ডিগ্রি (ঘ) ৬৫ ডিগ্রি

উত্তরঃ (ঘ) ৬৫ ডিগ্রি

Explanation:
আমরা জানি ,ত্রিভুজের তিন কোণের সমষ্টি ১৮০ ডিগ্রি । একটি সমদ্বিবাহু ত্রিভুজের একটি কোণের পরিমাণ ৫০ ডিগ্রি হলে অপর দুটি কোণের সমষ্টি হবে ১৮০-৫০ = ১৩০ ডিগ্রি । অপর দুটি কোণের প্রত্যেকটির পরিমাণ হবে-- ১৩০÷ ২=৬৫ ডিগ্রি

৩৫. একটি ত্রিভুজ আঁকা সম্ভব তখনই যখন ত্রিভুজটির দুইবাহুর যোগফল-- [উপজেলা নির্বাচন অফিসার-২০০৮]

(ক) তৃতীয় বাহুর সমান (খ) তৃতীয় বাহু অপেক্ষা ক্ষুদ্রতর (গ) তৃতীয় বাহু অপেক্ষা বৃহত্তর (ঘ) কোনটিই নয়

উত্তরঃ (গ) তৃতীয় বাহু অপেক্ষা বৃহত্তর

৩৬. কোন ত্রিভুজের তিনটি বাহুকে বর্ধিত করলে উৎপন্ন বহিঃস্থ কোণ তিনটির সমষ্টি কত? [ প্রাক প্রাথমিক সহকারী শিক্ষক-২০১৩(যমুনা)]

(ক) ১৮০ ডিগ্রি (খ) ২৭০ ডিগ্রি (গ) ৩৬০ ডিগ্রি (ঘ) ৫৪০ ডিগ্রি

উত্তরঃ (গ) ৩৬০ ডিগ্রি

Explanation:
কোনো ত্রিভুজের অন্তঃস্থ তিন কোণের সমষ্টি ১৮০ ডিগ্রি ।ত্রিভুজের তিনটি বাহুকে একইভাবে বর্ধিত করলে প্রত্যেক বাহুর উপর যে অন্তঃস্থ ও বহিঃস্থ কোণ উৎপন্ন হয় তাদের সমষ্টি ১৮০ ডিগ্রি হয়। অতএব, তিনটি বাহুর উপর উৎপন্ন কোণের সমষ্টি হয় ১৮০ × ৩ = ৫৪০ ডিগ্রি ।সুতরাং উৎপন্ন বহিঃস্থ কোণ তিনটির সমষ্টি হবে (৫৪০-১৮০) বা ৩৬০ ডিগ্রি ।

৩৭. তিনটি বাহুর দৈর্ঘ্য সেন্টিমিটারে দেয়া হল। কোন ক্ষেত্রে ত্রিভুজ অঙ্কন সম্ভব? [রেলওয়ে উপ সহকারী-২০১৩]

(ক) ২, ৫ ও ৮ (খ) ৫, ৪ ও ৯ (গ) ৩, ৪ ও ৫ (ঘ) সকল ক্ষেত্রে

উত্তরঃ (গ) ৩, ৪ ও ৫

Explanation:
এখানে দেখতে হবে একটি বাহুকে বর্গ করে যদি অপর দুই বাহুর বর্গের সমষ্টির সমান হয় তাহলেই কেবল ত্রিভুজ অঙ্কন করা সম্ভব।

৩৮. সমকোণী ত্রিভুজের অতিভুজ সংলগ্ন কোণ দুটির প্রত্যেকটি- [ প্রাক প্রাথমিক সহকারী শিক্ষক-২০১৩(শীতলক্ষ্যা)]

(ক) সরলকোণ (খ) সূক্ষ্মকোণ (গ) পূরক কোণ (ঘ) স্থূল কোণ

উত্তরঃ (খ) সূক্ষ্মকোণ

Explanation:
সমকোণী ত্রিভুজের একটি কোণ সমকোণ এবং অপর দুটি কোণ সূক্ষ্মকোণ।

৩৯ . ABC ত্রিভুজে AB = AC এবং ∠C = ৩০ ডিগ্রি হলে ∠A এর পরিমাণ- [২১ তম বিসিএস]

(ক) ৩০ ডিগ্রি (খ) ৯৫ ডিগ্রি (গ) ৯০ ডিগ্রি (ঘ) ১২০ ডিগ্রি

উত্তরঃ (ঘ) ১২০ ডিগ্রি

Explanation:
সমদ্বিবাহু ত্রিভুজের দুটি কোণ সমান হয়।তাই ∠C = ৩০ ডিগ্রি হলে ∠B ও ৩০ ডিগ্রি । সুতরাং ∠A এর পরিমাণ = ১৮০-(৩০+৩০) = ১৮০-৬০ =১২০ ডিগ্রি ।

৪০. ত্রিভুজের যে কোন দুই বাহুর মধ্যবিন্দুর সংযোজক সরলরেখা তৃতীয় বাহুর--- [ প্রাথমিক সহকারী শিক্ষক-২০১১( শাপলা)]

(ক) সমান হবে (খ) বড় হবে (গ) দ্বিগুণ হবে (ঘ) অর্ধেক হবে

উত্তরঃ (ঘ) অর্ধেক হবে

৪১. সমকোণী ত্রিভুজের একটি কোণ ৯০ ডিগ্রি হলে, অপর দুটি কোণের মান কত? ...

(ক) ১৮০ ডিগ্রি (খ) ১৯০ ডিগ্রি (গ) ২৭০ ডিগ্রি (ঘ) ৯০ ডিগ্রি

উত্তরঃ (ঘ) ৯০ ডিগ্রি

Explanation:
যেহেতু ত্রিভুজের তিনকোণের সমষ্টি ১৮০ ডিগ্রি সেহেতু অপর দুটি কোণের মান হবে = ১৮০-৯০ = ৯০ ডিগ্রি ।

৪২. সমকোণী ত্রিভুজের বাহুগুলোর অনুপাত কত? [ এলজিআরডির সহকারী প্রকৌশলী-২০০৫]

(ক) ৬ : ৪ : ৩ (খ) ৬ : ৫ : ৪ (গ) ১২ : ৮ : ৪ (ঘ) ১৩ : ১২ : ৫

উত্তরঃ (ঘ) ১৩ : ১২ : ৫

Explanation:
এখানে দেখতে হবে কোন অপশনটিতে কোন একটি বাহুকে বর্গ করে অপর দুই বাহুর বর্গের সমষ্টির সমান হয় কি না?

৪৩. ≅ এই প্রতিকের অর্থ হল? [১৭ তম বিসিএস]

(ক) আকার ও আকৃতি সমান (খ) আকার ও পরিমাণ সমান (গ) আকার ও আকৃতি সমান নয় (ঘ) আকার ও আকৃতি ও পরিমাণ সমান

উত্তরঃ (ক) আকার ও আকৃতি সমান

৪৪. তিন কোণ দেয়া থাকলে যে সকল ত্রিভুজ আঁকা যায় সেগুলোকে কি ত্রিভুজ বলে? [ প্রাথমিক সহকারী শিক্ষক-২০১২(মেঘনা)]

(ক) সমান ত্রিভুজ (খ) সর্বসম ত্রিভুজ (গ) সদৃশ ত্রিভুজ (ঘ) সমানুপাতিক ত্রিভুজ

উত্তরঃ (গ) সদৃশ ত্রিভুজ

৪৫. দুটি ত্রিভুজের মধ্যে কোন উপাদান গুলো সমান হওয়া সত্তে¡ও ত্রিভুজ দুটি সর্বসম নাও হতে পারে? [প্রাথমিক সহকারী শিক্ষক-২০০৮(পদ্মা)]

(ক) দুইটি বাহু ও এক কোণ (খ) তিনটি বাহু (গ) এক বাহু এবং দুই কোণ (ঘ) তিন কোণ

উত্তরঃ (ঘ) তিন কোণ

Explanation:
দুৃটি ত্রিভুজের সর্বসম হওয়ার শর্ত হলো তিনটি কোণ ও তিনটি বাহু সমান হওয়া। শুধুমাত্র তিনটি কোণ সমান হলে সর্বসম না ও হতে পারে।

৪৬. দুইটি ত্রিভুজ সর্বসম হওয়ার জন্য নিচের কোন শর্তটি যথেষ্ট নয়? [বিআরসি - এর অফিসার-১৯৯৭]

(ক) একটির তিনবাহু অপরটির তিনবাহুর সমান (খ) একটির তিনকোণ অপরটির তিনকোণের সমান (গ) একটির দুই কোণ ও একবাহু অপরটির দুইকোণ ও অনুরূপ বাহুর সমান (ঘ) একটির দুইবাহু ও অন্তর্ভূক্ত কোণ অপরটির দুইবাহু ও অন্তর্ভূক্ত কোণের সমান

উত্তরঃ (খ) একটির তিনকোণ অপরটির তিনকোণের সমান

৪৭. ত্রিভুজ ABC- এ, ABC কোণ = ৯০ ডিগ্রি , AB = ৪ সেমি এবং BC = ৩ সেমি। AC বাহুর দৈর্ঘ্য কত? [দুর্নীতি দমন পরিদর্শক -২০০৪]

(ক) ৫ সেমি (খ) ৩.৫ সেমি (গ) ২ সেমি (ঘ) ৪.৫ সেমি

উত্তরঃ (ক) ৫ সেমি

Explanation:
যেহেতু ত্রিভুজটি সমকোণী ত্রিভুজ। তাই এখানে দেখতে হবে ৪ ও ৩ এর বর্গের সমষ্টি কোন অপশনটির বর্গের সমষ্টি হয় ।৪ ও ৩ এর বর্গের সমষ্টি = ১৬+৯ = ২৫। অপশন ক এর ৫ কে বর্গ করলে হয় ২৫। তাই অপশন ক ই সঠিক উত্তর।

৪৮. কোন ত্রিভুজের শীর্ষবিন্দু হতে বিপরীত বাহুর মধ্যবিন্দুর উপর অঙ্কিত রেখাকে ঐ ত্রিভুজের কি বলা হয়? [ প্রাক প্রাথমিক সহকারী শিক্ষক(২৭.০৬.২০১৫)]

(ক) মধ্যমা (খ) ভূমি (গ) অতিভুজ (ঘ) লম্ব

উত্তরঃ (ক) মধ্যমা

Explanation:
কোন ত্রিভুজের শীর্ষবিন্দু হতে বিপরীত বাহুর মধ্যবিন্দুর উপর অঙ্কিত রেখাকে ঐ ত্রিভুজের মধ্যমা বলা হয়।

৪৯. ত্রিভুজের বৃহত্তর বাহু সংলগ্ন কোণদ্বয়-- [ প্রাক প্রাথমিক সহকারী শিক্ষক-২০১৪(বিটা)]

(ক) সূক্ষ্মকোণ (খ) স্থুলকোণ (গ) সমকোণ (ঘ) সরলকোণ

উত্তরঃ (ক) সূক্ষ্মকোণ

৫০. ত্রিভুজের তিন কোণের সমষ্টি দুই সমকোণের সমান--কোন ক্ষেত্রে সত্য? [ প্রাথমিক সহকারী শিক্ষক-২০০৬(বরিশাল)]

(ক) শুধু সূক্ষ্মকোণী ত্রিভুজের ক্ষেত্রে (খ) শুধু স্থুলকোণী ত্রিভুজের ক্ষেত্রে (গ) শুধু সমকোণী ত্রিভুজের ক্ষেত্রে (ঘ) সকল ত্রিভুজের ক্ষেত্রে

উত্তরঃ (ঘ) সকল ত্রিভুজের ক্ষেত্রে

৫১. একটি ত্রিভুজের একটি কোণ যদি ২য় কোণের তিনগুণ এবং ৩য় কোণ যদি ২য় কোণের চেয়ে ৩০ ডিগ্রি বড় হয় তবে কোণটি কত ডিগ্রি? [ প্রাক প্রাথমিক সহকারী শিক্ষক(৩০.১০.২০১৫)]

(ক) ৬০ ডিগ্রি (খ) ৫০ ডিগ্রি (গ) ৪৫ ডিগ্রি (ঘ) ৩০ ডিগ্রি

উত্তরঃ (ক) ৬০ ডিগ্রি

Explanation:
আমরা জানি, ত্রিভুজের তিন কোণের সমষ্টি = ১৮০ ডিগ্রি ।
ধরি, ২য় কোণ ক
১ম কোণ ৩ক
এবং ৩য় কোণ ক+৩০ ডিগ্রি
শর্তমতে, ক+ ৩ক +ক + ৩০ = ১৮০
বা, ৫ক = ১৮০-৩০
বা, ৫ক = ১৫০
বা, ক = ১৫০ ÷ ৫ = ৩০
সুতরাং ১ম কোণ = ৩ × ৩০ = ৯০ ডিগ্রি
২য় কোণ = ৩০ ডিগ্রি
৩য় কোণ = ৩০ + ৩০ = ৬০ ডিগ্রি

৫২. সমকোণী ত্রিভুজের সমকোণ সংলগ্ন বাহুদ্বয় যথাক্রমে ৩ ও ৪ সেমি হলে,এর অতিভুজের মান কত? [ প্রাক প্রাথমিক সহকারী শিক্ষক-২০১৩(করতোয়া)]

(ক) ৭ সেমি (খ) ৮ সেমি (গ) ৪ সেমি (ঘ) ৫ সেমি

উত্তরঃ (ঘ) ৫ সেমি

Explanation:
আমরা জানি, সমকোণী ত্রিভুজের
${(অতিভুজ)}^{২} = {(ভুমি)}^{২} + {(লম্ব)}^{২}$
বা, ${(অতিভুজ)}^{২} = ৩^{২} + ৪^{২}$
বা, ${(অতিভুজ)}^{২} = ৯ + ১৬$
বা, ${(অতিভুজ)}^{২} = ২৫$
সুতরাং অতিভুজ = ৫ [ বর্গমূল করে]

৫৩. সমকোণী ত্রিভুজের সমকোণের বিপরীত একটি কোণ ৫০ ডিগ্রি হলে অপর কোণটি কত? [প্রাথমিক সহকারী শিক্ষক-২০১২]

(ক) ৪০ ডিগ্রি (খ) ৫০ ডিগ্রি (গ) ২০ ডিগ্রি (ঘ) ৩০ ডিগ্রি

উত্তরঃ (ক) ৪০ ডিগ্রি

Explanation:
আমরা জানি, ত্রিভুজের তিন কোণের সমষ্টি = ১৮০ ডিগ্রি ।সমকোণী ত্রিভুজের একটি কোণ সমকোণ থাকে এবং আরেকটি কোণ দেওয়া আছে ৫০ ডিগ্রি। অপর কোণ = ১৮০- (৫০+৯০) = ১৮০- ১৪০ = ৪০ ডিগ্রি ।

৫৪. ত্রিভুজের তিন বাহুর উপর অঙ্কিত বর্গক্ষেত্রসমুহ কয়টি সমকোণ তৈরি করে? [ প্রাথমিক সহকারী শিক্ষক( ১১.০৬.২০১৮)]

(ক) ১২ (খ) ১৬ (গ) ৮ (ঘ) ৯

উত্তরঃ (ক) ১২

Explanation:
এখানে, তিন বাহুর উপর তিনটি বর্গক্ষেত্র আঁকা যায়।
এখন, ১ বর্গক্ষেত্র = ৪ টি সমকোণ
সুতরাং ৩ বর্গক্ষেত্র = ৪ × ৩ = ১২ টি সমকোণ

৫৫. সমকোণী ত্রিভুজের অতিভুজের দৈর্ঘ্য দেয়া থাকলে--- [ প্রাক প্রাথমিক সহকারী শিক্ষক-২০১৪(আলফা)]

(ক) একটি ত্রিভুজ আকা যায় (খ) দুটি ত্রিভুজ আকা যায় (গ) তিনটি ত্রিভুজ আকা যায় (ঘ) অনেকগুলো ত্রিভুজ আ্কা যায়

উত্তরঃ (ঘ) অনেকগুলো ত্রিভুজ আ্কা যায়

Explanation:
একটি ত্রিভুজ আঁকতে হলে ন্যূনতম একটি কোণ ও বাহু থাকতে হবে। সেক্ষেত্রে সমকোণী ত্রিভুজের অতিভুজ দেওয়া থাকলে ত্রিভুজ অঙ্কন করা সম্ভব । অতিভুজের দৈর্ঘ্যকে ঠিক রেখে লম্ব ও ভূমি বাহুকে ঠিক রেখে অনেকগুলু ত্রিভুজ আঁকা যাবে ।

৫৬. একটি ত্রিভুজের মধ্যমাত্রয় সমান হলে ত্রিভুজটি--- [ প্রাক প্রাথমিক সহকারী শিক্ষক-২০১৪(ডেলটা)]

(ক) সমদ্বিবাহু (খ) সমবাহু (গ) বিষমবাহু (ঘ) স্থুলকোণী

উত্তরঃ (খ) সমবাহু

Explanation:
ত্রিভুজের যে কোন দুটি মধ্যমা পরস্পর সমান হলে ত্রিভুজটি সমদ্বিবাহু হয় এবং ত্রিভুজের তিনটি মধ্যমা বা মধ্যমাত্রয় পরস্পর সমান হলে ত্রিভুজটি সমবাহু হয়।

৫৭. সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য ৬ মিটার হলে,ক্ষেত্রফল কত? [ প্রাথমিক প্রধান শিক্ষক-২০০৯(শিউলী)]

(ক) ৮√৩ বর্গমিটার (খ) ৯√৩ বর্গমিটার (গ) ১২√৩ বর্গমিটার (ঘ) ১৬ বর্গমিটার

উত্তরঃ (খ) ৯√৩ বর্গমিটার

Explanation:
ধরি , সমবাহু ত্রিভুজের বাহুর দৈঘ্য = a
তাহলে , সমবাহু ত্রিভুজের ক্ষেত্রফল = $\frac{√৩}{৪} a^{২}$
= $\frac{√৩}{৪} {(৬)}^{২}$
= $\frac{√৩}{৪} \times ৩৬$
= ৯√৩

৫৮. ত্রিভুজের তিন বাহু, উহার অন্তঃবৃত্তের----- [ প্রাক প্রাথমিক সহকারী শিক্ষক-২০১৩]

(ক) জ্যা (খ) ব্যাস (গ) ব্যাসার্ধ (ঘ) স্পর্শক

উত্তরঃ (ঘ) স্পর্শক

Explanation:
কোন ত্রিভুজের তিনবাহু ত্রিভুজটিতে অন্তর্লিখিত বৃত্তের স্পর্শক হয়। যেকোন ত্রিভুজে অন্তস্থ বৃত্তটি ত্রিভুজের তিনবাহু স্পর্শ করে থাকে এবং যে বিন্দুতে বৃত্তটি বাহুকে স্পর্শ করে ঐ বিন্দুকে বলা হয় স্পর্শবিন্দু।

৫৯. একটি সমকোণী ত্রিভুজের ক্ষেত্রফল ১৪৪ বর্গ একক।সমকোণ সন্নিহিত বাহুদ্বয়ের একটির দৈর্ঘ্য ১২ একক হলে অপরটি কত? [ প্রাথমিক সহকারী শিক্ষক-২০০৬(পিইডিপি-২)]

(ক) ১৫ একক (খ) ২৪ একক (গ) ২০ একক (ঘ) ৩০ একক

উত্তরঃ (খ) ২৪ একক

Explanation:
সমকোণী ত্রিভুজের ক্ষেত্রফল = $\frac{১}{২}$ × সন্নিহিত বাহুদ্বয়ের গুণফল
প্রশ্নমতে, $\frac{১}{২}$ × ১২ × অপর বাহু = ১৪৪
বা, ৬ × অপর বাহু = ১৪৪
বা, অপর বাহু = ১৪৪ ÷ ৬
বা, অপর বাহু =২৪ একক

৬০. ত্রিভুজের যে কোনো বাহুকে উভয়দিকে বর্ধিত করলে উৎপন্ন বহিঃস্থ কোণদ্বয়ের সমষ্টি------ [প্রাথমিক সহকারী শিক্ষক-২০১২(যমুনা)]

(ক) দুই সমকোণ অপেক্ষা ক্ষুদ্রতর (খ) দুই সমকোণ অপেক্ষা বৃহত্তর (গ) দুই সমকোণের সমান (ঘ) দুই সমকোণের অর্ধেক

উত্তরঃ (খ) দুই সমকোণ অপেক্ষা বৃহত্তর

৬১. কোনো ত্রিভুজের শিরঃকোণের সমদ্বিখন্ডক যদি ভুমির উপর লম্ব হয়,তবে ত্রিভুজটিকে কি বলে? [ প্রাথমিক সহকারী শিক্ষক-২০১২(পদ্মা)]

(ক) সমদ্বিবাহু (খ) সমবাহু (গ) সমকোণী (ঘ) স্থুলকোণী

উত্তরঃ (ক) সমদ্বিবাহু

৬২. কোন ত্রিভুজের মধ্যমা তিনটি যে বিন্দুতে ছেদ করে তাকে বলে---- [ প্রাক প্রাথমিক সহকারী শিক্ষক-২০১৩(সুরমা)]

(ক) ভরকেন্দ্র (খ) অন্তঃকেন্দ্র (গ) পরিকেন্দ্র (ঘ) লম্ববিন্দু

উত্তরঃ (ক) ভরকেন্দ্র

৬৩. কোন ত্রিভুজের বাহুগুলোর লম্ব-দ্বিখন্ডক তিনটি যে বিন্দুতে ছেদ করে তাকে বলে- [ প্রাক প্রাথমিক সহকারী শিক্ষক-২০১৩(বুড়িগঙ্গা) ]

(ক) ভরকেন্দ্র (খ) পরিকেন্দ্র (গ) অন্তঃকেন্দ্র (ঘ) লম্ববিন্দু

উত্তরঃ (খ) পরিকেন্দ্র

৬৪. ত্রিভুজের ভরকেন্দ্র প্রত্যেক মধ্যমাকে কোন অনুপাতে অন্তর্বিভক্ত করে? [ প্রাথমিক প্রধান শিক্ষক-২০০৯(শাপলা)]

(ক) ২:১ (খ) ৩:১ (গ) ১:২ (ঘ) ১:৩

উত্তরঃ (ক) ২:১

Explanation:
ত্রিভুজের মধ্যমাত্রয় যে বিন্দুতে মিলিত হয় তাকে ভরকেন্দ্র বলে। ভরকেন্দ্র মধ্যমাকে ২ঃ১ অনুপাতে অন্তর্বিভক্ত করে।

৬৫. ত্রিভুজের দুইটি কোণের সমষ্টি তৃতীয় কোণের সমান হলে ত্রিভুজটি---- [প্রাক প্রাথমিক সহকারী শিক্ষক-২০১৩(সুরমা)]

(ক) সমবাহু (খ) সমদ্বিবাহু (গ) সমকোণী (ঘ) কোনোটিই নয়

উত্তরঃ (গ) সমকোণী

Explanation:
ত্রিভুজের তিন কোণের সমষ্টি দুই সমকোণ বা ১৮০ ডিগ্রি
সমকোণী ত্রিভুজের একটি কোণের মান ৯০ ডিগ্রি
এবং অন্য দুই কোণে মানের সমষ্টি ৯০ ডিগ্রি

৬৬. ত্রিভুজের একটি বাহু বর্ধিত করলে বহিঃস্থ কোণটি--- [ প্রাথমিক সহকারী শিক্ষক-২০০৬(রাজশাহী)]

(ক) বিপরীত অন্তঃস্থ কোণদ্বয়ের সমষ্টি অপেক্ষা বড় হবে (খ) বিপরীত অন্তঃস্থ কোণদ্বয়ের সমষ্টি অপেক্ষা ছোট হবে (গ) বিপরীত অন্তঃস্থ কোণদ্বয়ের সমষ্টির সমান হবে (ঘ) বিপরীত অন্তঃস্থ কোণদ্বয়ের সমষ্টির দ্বিগুণ হবে

উত্তরঃ (গ) বিপরীত অন্তঃস্থ কোণদ্বয়ের সমষ্টির সমান হবে

Explanation:
ত্রিভুজের বহিঃস্থ কোণ সম্পর্কিত দুটি অনুসিদ্ধান্ত,
১। ত্রিভুজের কোন এক বাহু বর্ধিত করলে যে বহিঃস্থ কোণ উৎপন্ন হয়, তা অন্তঃস্থ বিপরীত কোণদ্বয়ের প্রত্যেকের চেয়ে বৃহত্তর।
২। ত্রিভুজের কোন এক বাহু বর্ধিত করলে যে বহিঃস্থ কোণ উৎপন্ন হয়, তা বিপরীত অন্তঃস্থ কোণদ্বয়ের সমষ্টির সমান

৬৭. একটি সমবাহু ত্রিভুজের একটি বাহু ১০ মিটার। ত্রিভুজটির ক্ষেত্রফল হবে- [ প্রাথমিক প্রধান শিক্ষক(পদ্ম)-২০০৯]

(ক) ১০√৩ বর্গমিটার (খ) ১৫ বর্গমিটার (গ) ২০ বর্গমিটার (ঘ) ২৫√৩ বর্গমিটার

উত্তরঃ (ঘ) ২৫√৩ বর্গমিটার

Explanation:
ধরি , সমবাহু ত্রিভুজের বাহুর দৈঘ্য = a
তাহলে , সমবাহু ত্রিভুজের ক্ষেত্রফল = $\frac{√৩}{৪} a^{২}$
= $\frac{√৩}{৪} {(১০)}^{২}$
= $\frac{√৩}{৪} \times ১০০$
= ২৫√৩

ত্রিভুজ কাকে বলে? ত্রিভুজ কত প্রকার ও কি কি? mcq সহ এ টু জেড

প্রাথমিক আলোচনা

ত্রিভুজ বিষয়ক গুরুত্বপূর্ণ অনুসিদ্ধান্ত

ত্রিভুজের সর্বসমতা

ত্রিভুজের কেন্দ্র

ত্রিভুজের প্রকারভেদ

সমকোণী ত্রিভুজ (Right angled triangle):

সমকোণী ত্রিভুজের বৈশিষ্ট্যঃ

• বাহুর মাধ্যমে চেনার উপায়:

পীথাগোরাসের উপপাদ্য:

সূক্ষ্মকোণী ত্রিভুজ (Acute Angled Triangle):

সূক্ষকোণী ত্রিভূজের বৈশিষ্ট্য:

স্থূলকোণী ত্রিভুজ (Obtuse Angled Triangle) :

স্থূলকোণী ত্রিভূজের বৈশিষ্ট্য:

সমবাহু ত্রিভুজ (Equilateral Triangle):

সমবাহু ত্রিভুজের বৈশিষ্ট্য:

সমবাহু ত্রিভুজের সুত্র:

সমদ্বিবাহু ত্রিভুজ (Isosceles Triangle):

সমদ্বিবাহু ত্রিভুজের বৈশিষ্ট্য:

বিষমবাহু ত্রিভুজ (Scalene Triangle):

বিষমবাহু ত্রিভুজের বৈশিষ্ট্য:

বিভিন্ন প্রতিযোগিতামূলক পরীক্ষার প্রশ্ন ও সমাধান

১. ১৭ সে.মি., ১৫ সে.মি., ৮ সে.মি. বাহু বিশিষ্ট ত্রিভুজটি হবে- [ কারা তত্ত্বাবধায়ক-২০১৯]

২. ΔABC এ ∠A = ৪০ ডিগ্রি, ∠B = ৭০ ডিগ্রি, হলে ΔABC কি ধরনের ত্রিভুজ? [সাব রেজিস্ট্রার-২০০১]

৩.যদি সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য a হয়,তবে ক্ষেত্রফল কত হবে? [ প্রাক প্রাথমিক সহকারী শিক্ষক(ভলগা)-২০১৩]

৫. একটি সমকোণী ত্রিভুজের সমকোণ ছাড়া অন্য দুটি কি কোণ? [ রেজিঃ বেসরকারি প্রাথমিক সহকারী শিক্ষক-২০১১(টগর)]

৬. কোনো ত্রিভুজের তিন কোণের দ্বিখন্ডকগুলো যে বিন্দুতে ছেদ করে তাকে কি বলে? [ ১৪তম বিসিএস]

৮. একটি সমকোণী ত্রিভুজের ভূমি ৮ ফুট এবং লম্ব ৬ ফুট হলে অতিভুজের দৈর্ঘ্য কত? [২৭ তম বিসিএস]

৯. ⊿ABC- এর BC বাহুকে D পর্যন্ত বাড়ানো হল। ∠A = ৬০ ডিগ্রি এবং ∠B = ৯০ ডিগ্রি হলে, ∠ACD = কত? [ ৪০ তম বিসিএস]

১০. কোন ত্রিভুজের কোণত্রয়ের সমদ্বিখন্ডকের ছেদবিন্দুকে কি বলে? [ শ্রম অধিদপ্তর-২০১৩]

১১. কোন ত্রিভুজের দুটি কোণ ১০ ডিগ্রি ও ৮০ ডিগ্রি । ত্রিভুজটি-- [স্বরাষ্ট্র মন্ত্রণালয়ের প্রশাসনিক কর্মকর্তা-২০১৩]

১২. ত্রিভুজের ক্ষেত্রফল - [ অগ্রণী ব্যাংক অফিসার-২০০৮]

১৫. ত্রিভুজের যে কোন দুটি মধ্যমা পরস্পর সমান হলে ত্রিভুজটি? [প্রধানমন্ত্রীর কার্যালয়ের সহকারী পরিচালক-২০০৮]

১৮. একটি সমবাহু ত্রিভুজের একটি বাহু ১৬ মিটার। ত্রিভুজটির ক্ষেত্রফল কত? [প্রাক প্রাথমিক সহকারী শিক্ষক(গামা)-২০১৪]

১৯. অতিভূজের বিপরীতে থাকে-- [ প্রাক প্রাথমিক সহকারী-২০১৩]

২০. একটি সমবাহু ত্রিভুজের এক বাহুর দৈর্ঘ্য ৪ সে : মি : হলে, উহার ক্ষেত্রফল হবে কত? [ পরিবার পরিকল্পনা কমকতা-২০০৯]

২১. একটি কোণের মান তার পূরক কোণের মানের অর্ধেকের সমান। কোণটির মান কত? [ প্রাথমিক সহকারী শিক্ষক-২০১২]

২২. সমদ্বিবাহু ত্রিভুজের সমান বাহুদ্বয় বর্ধিত করলে উৎপন্ন কোণদ্বয় হবে-- [প্রাক প্রাথমিক সহকারী শিক্ষক(গামা)-২০১৪]

২৬. একটি সমকোণী ত্রিভুজের দ্বিতীয় কোণটির মাপ ২০ ডিগ্রি হলে তৃতীয় কোণটির মাপ-- [ প্রাক প্রাথমিক সহকারী শিক্ষক-২০১৩]

২৭. ABC ত্রিভুজে AB = AC , ∠A = ৮০ ডিগ্রি , ∠B = কত? [ সাব রেজিঃ -২০০১]

২৮. একটি সমকোণী সমদ্বিবাহু ত্রিভুজের তিন কোণের পরিমাণ--- [তথ্য সহকারী-২০১৩]

৩০. সমবাহু ত্রিভুজের প্রত্যেকটি কোণের পরিমাণ কত? [ বাণিজ্য সহকারী পরিচালক-২০১৩]

৩১. যে ত্রিভুজের দুটি বাহু পরস্পর সমান, তা--- [ মাদক অধিদপ্তর -২০১৩]

৩২. কোনো ত্রিভুজের একটি কোণ অপর দুটি কোণের সমান হলে ত্রিভুজটি --- [ খাদ্য অধিদপ্তর পরিদর্শক-২০১২]

৩৩. কোন ত্রিভুজের তিন বাহুর সমদ্বিখন্ডকগুলোর ছেদবিন্দুর নাম কি? [ প্রাথমিক প্রধান শিক্ষক-২০১২(ক্যামেলিয়া)]

৩৫. একটি ত্রিভুজ আঁকা সম্ভব তখনই যখন ত্রিভুজটির দুইবাহুর যোগফল-- [উপজেলা নির্বাচন অফিসার-২০০৮]

৩৭. তিনটি বাহুর দৈর্ঘ্য সেন্টিমিটারে দেয়া হল। কোন ক্ষেত্রে ত্রিভুজ অঙ্কন সম্ভব? [রেলওয়ে উপ সহকারী-২০১৩]

৩৮. সমকোণী ত্রিভুজের অতিভুজ সংলগ্ন কোণ দুটির প্রত্যেকটি- [ প্রাক প্রাথমিক সহকারী শিক্ষক-২০১৩(শীতলক্ষ্যা)]

৩৯ . ABC ত্রিভুজে AB = AC এবং ∠C = ৩০ ডিগ্রি হলে ∠A এর পরিমাণ- [২১ তম বিসিএস]

৪০. ত্রিভুজের যে কোন দুই বাহুর মধ্যবিন্দুর সংযোজক সরলরেখা তৃতীয় বাহুর--- [ প্রাথমিক সহকারী শিক্ষক-২০১১( শাপলা)]

৪১. সমকোণী ত্রিভুজের একটি কোণ ৯০ ডিগ্রি হলে, অপর দুটি কোণের মান কত? ...

৪২. সমকোণী ত্রিভুজের বাহুগুলোর অনুপাত কত? [ এলজিআরডির সহকারী প্রকৌশলী-২০০৫]

৪৩. ≅ এই প্রতিকের অর্থ হল? [১৭ তম বিসিএস]

৪৪. তিন কোণ দেয়া থাকলে যে সকল ত্রিভুজ আঁকা যায় সেগুলোকে কি ত্রিভুজ বলে? [ প্রাথমিক সহকারী শিক্ষক-২০১২(মেঘনা)]

৪৬. দুইটি ত্রিভুজ সর্বসম হওয়ার জন্য নিচের কোন শর্তটি যথেষ্ট নয়? [বিআরসি - এর অফিসার-১৯৯৭]

৪৭. ত্রিভুজ ABC- এ, ABC কোণ = ৯০ ডিগ্রি , AB = ৪ সেমি এবং BC = ৩ সেমি। AC বাহুর দৈর্ঘ্য কত? [দুর্নীতি দমন পরিদর্শক -২০০৪]

৪৯. ত্রিভুজের বৃহত্তর বাহু সংলগ্ন কোণদ্বয়-- [ প্রাক প্রাথমিক সহকারী শিক্ষক-২০১৪(বিটা)]

৫০. ত্রিভুজের তিন কোণের সমষ্টি দুই সমকোণের সমান--কোন ক্ষেত্রে সত্য? [ প্রাথমিক সহকারী শিক্ষক-২০০৬(বরিশাল)]

৫৩. সমকোণী ত্রিভুজের সমকোণের বিপরীত একটি কোণ ৫০ ডিগ্রি হলে অপর কোণটি কত? [প্রাথমিক সহকারী শিক্ষক-২০১২]

৫৪. ত্রিভুজের তিন বাহুর উপর অঙ্কিত বর্গক্ষেত্রসমুহ কয়টি সমকোণ তৈরি করে? [ প্রাথমিক সহকারী শিক্ষক( ১১.০৬.২০১৮)]

৫৫. সমকোণী ত্রিভুজের অতিভুজের দৈর্ঘ্য দেয়া থাকলে--- [ প্রাক প্রাথমিক সহকারী শিক্ষক-২০১৪(আলফা)]

৫৬. একটি ত্রিভুজের মধ্যমাত্রয় সমান হলে ত্রিভুজটি--- [ প্রাক প্রাথমিক সহকারী শিক্ষক-২০১৪(ডেলটা)]

৫৭. সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য ৬ মিটার হলে,ক্ষেত্রফল কত? [ প্রাথমিক প্রধান শিক্ষক-২০০৯(শিউলী)]

৫৮. ত্রিভুজের তিন বাহু, উহার অন্তঃবৃত্তের----- [ প্রাক প্রাথমিক সহকারী শিক্ষক-২০১৩]

৬২. কোন ত্রিভুজের মধ্যমা তিনটি যে বিন্দুতে ছেদ করে তাকে বলে---- [ প্রাক প্রাথমিক সহকারী শিক্ষক-২০১৩(সুরমা)]

৬৪. ত্রিভুজের ভরকেন্দ্র প্রত্যেক মধ্যমাকে কোন অনুপাতে অন্তর্বিভক্ত করে? [ প্রাথমিক প্রধান শিক্ষক-২০০৯(শাপলা)]

৬৫. ত্রিভুজের দুইটি কোণের সমষ্টি তৃতীয় কোণের সমান হলে ত্রিভুজটি---- [প্রাক প্রাথমিক সহকারী শিক্ষক-২০১৩(সুরমা)]

৬৬. ত্রিভুজের একটি বাহু বর্ধিত করলে বহিঃস্থ কোণটি--- [ প্রাথমিক সহকারী শিক্ষক-২০০৬(রাজশাহী)]

৬৭. একটি সমবাহু ত্রিভুজের একটি বাহু ১০ মিটার। ত্রিভুজটির ক্ষেত্রফল হবে- [ প্রাথমিক প্রধান শিক্ষক(পদ্ম)-২০০৯]

W3classroom Online School